卷积神经网络CNN

YaHei 4月 18, 2018

BGM：《四月是你的谎言》ED2

参考：

CNN原理

卷积神经网络主要由卷积层+激活函数+池化层组成，并且在最后用全连接层输出——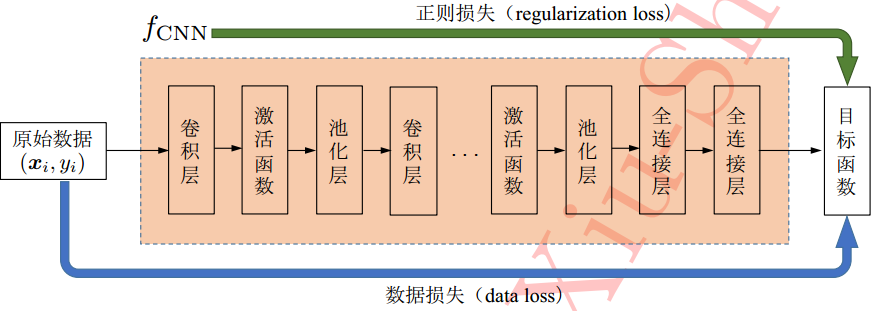
12CNN

反向传播

机器学习-吴恩达/3 非线性分类器——神经网络/反向传播算法 | Hey~YaHei!
论文：Learning representation by back-propagating errors(1986)

前向传播：
$$ z_i = \omega_i^T x_{i} $$
其中，
$z_i$ 为第i层的损失，即 $z_i = Cost(x_{i+1}, y)$；
$x_i$ 为第i层的输入；
$\omega_i$ 为第i层的参数；
$x_0$ 为原始输入

根据链式法则，$z_i$ 对参数 $\omega_i$ 和输入 $x_i$ 求偏导——
$$ \frac{\partial z_i}{\partial \omega_i} = \frac{\partial z_i}{\partial x_{i+1}} \frac{\partial x_{i+1}}{\partial \omega_i} $$
$$ \frac{\partial z_i}{\partial x_i} = \frac{\partial z_i}{\partial x_{i+1}} \frac{\partial x_{i+1}}{\partial x_i} $$
其中，
由于 $x_{i+1}$ 由 $x_i$ 经过 $\omega_i$ 的作用得到，则 $\frac{\partial x_{i+1}}{\partial \omega_i}$ 和 $\frac{\partial x_{i+1}}{\partial x_i}$ 可以直接求得；
剩下的部分 $\frac{\partial z_i}{\partial x_{i+1}}$ 是由后一层计算得到；

总的来说，误差由后往前传播，
$\frac{\partial z_i}{\partial \omega_i}$ 用于梯度下降，如 $\omega_i \gets \omega_i - \eta \frac{\partial z}{\partial \omega_i}$；
$\frac{\partial z_i}{\partial x_i}$ 用于前层 $\frac{\partial z_{i-1}}{\partial \omega_{i-1}}$ 的计算

这里对不同参数的求导操作非常繁琐，Theano、Tensorflow都采用符号微分的方法进行自动求导（编译时就计算得到导数的数学表示）；
具体可以参见“花书”《Deep Learning 深度学习》（中文版）P126-139

卷积层（Conv）

卷积层并不是使用严格数学意义的卷积运算，而是使用保留卷积性质但抛弃可交换性的互相关函数；
卷积运算具有可交换性，这在数学证明上是很有用的，但在神经网络的应用中却是一个比较鸡肋的性质
卷积操作选用一定大小的卷积核（下图黄色区域）在原始数据上移动，与重合部分数据做乘和运算；
依次类推，最终输出一张特征图（Feature Map）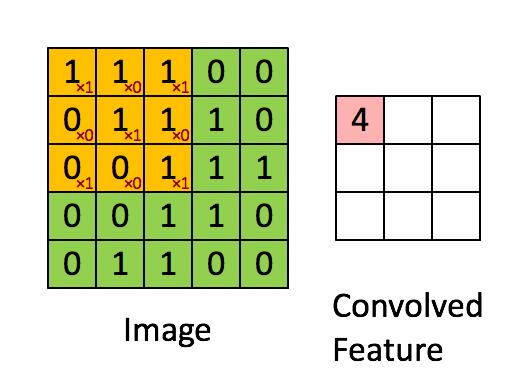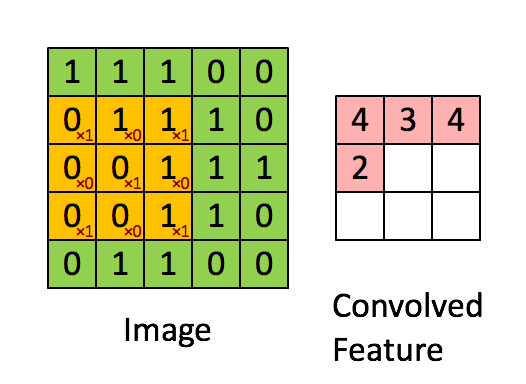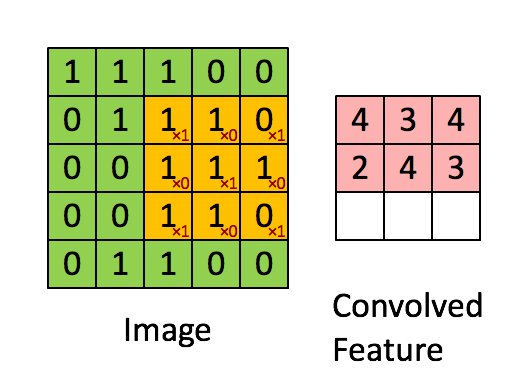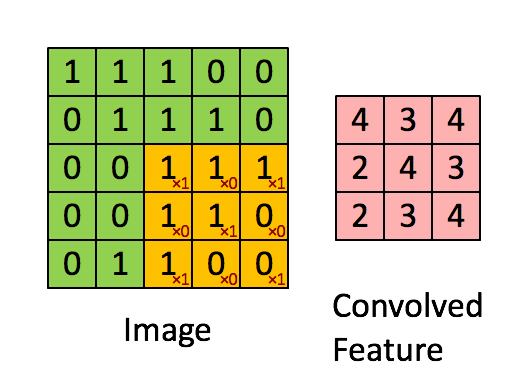
12Convolutional_Kernel

卷积核的作用相当一个滤波器，其参数是经过学习得到的，可以用于提取图片中的特征；
由于核参数是随机初始化的，所以它们很可能会提取出不同的特征；
由低层的卷积层提取简单特征，然后逐层堆叠卷积层，将简单特征逐渐抽象为更高层次的语义概念；

大核的卷积层可以用多层的小核的卷积层实现；
比如用三层3x3卷积核的卷积层可以提取到一层7x7卷积核的卷积层一样的特征——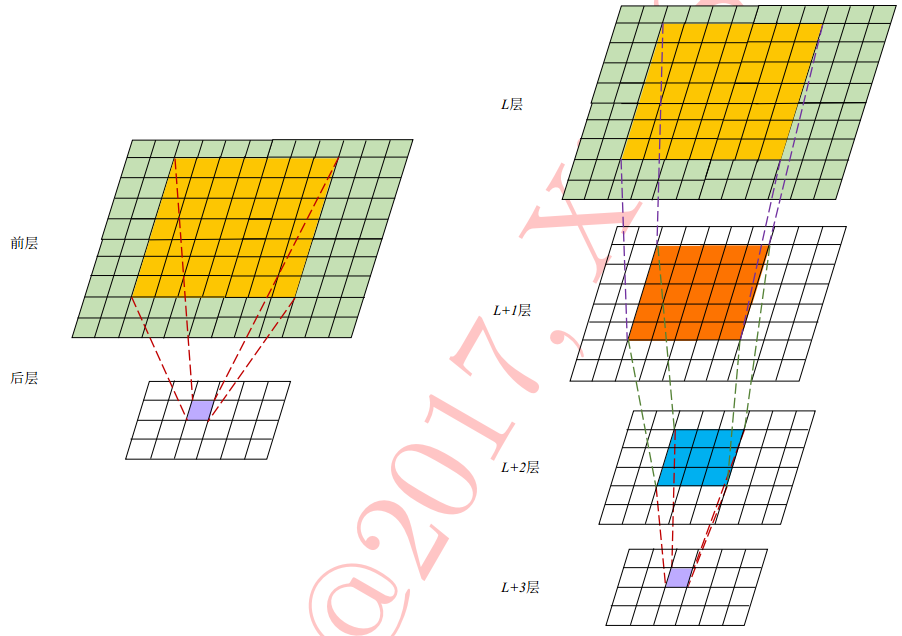
12Multi_Conv_Layers
而且，使用多层小核卷积层由以下优势：

减少参数
7x7卷积核有 $7 \times 7 = 49$ 个参数，而三层3x3卷积核只有 $3 \times 3 \times 3 = 27$ 个参数
增加网络深度
增加网络容量和复杂度

卷积操作的变体：

扩大原有卷积核在前层的感受野
论文：Deformable Convolutional Networks(2017)
感受野形状可变（而不再是简单的矩形区域）
论文：Multi-Scale Context Aggregation by Dilated Convolutions(2016)

池化层（Pool）

池化操作与卷积操作类似，但池化层是不需要参数的；
选用一定大小的池化核在原始数据上移动，与重合部分数据做一定的聚合运算（取均值、取最值、按一定概率随机取值等）；
依次类推，最终输出一张特征图；

详见《漫谈池化层 | Hey~YaHei!》

全连接层（Fully Connection）

参考：全连接层的作用是什么？——魏秀参的回答 | 知乎

全连接层在CNN中起“分类器”作用，将卷积层、池化层、激活函数学到的特征表示映射到样本的标记空间；
由于最后一层卷积层输出一个若干个二维数据（总体为三维），所以输入FC前通常需要将其展平（Flatten）为一维；

实际上，全连接层可以用卷积操作代为实现：

如果FC前为FC，则该FC可以转换成1 x 1的卷积
如果FC前为卷积层，则该FC可以转换为H x W的卷积（H、W为前层输出的高、宽）

由于全连接层参数冗余，一些网络如ResNet、GoogLeNet等采用全局平均池化（GAP）取代FC来融合学到的深度特征；

近期研究也发现，FC可以在模型表示能力迁移过程中（尤其是原任务与目标任务差异较大时）充当“防火墙”，保证模型表示能力的迁移；

tensorflow实现

卷积层

借助 tf.nn.conv2d() ——

import numpy as np
from sklearn.datasets import load_sample_images

# 读入一些图片
dataset = np.array(load_sample_images().images, dtype=np.float32)
batch_size, height, width, channels = dataset.shape

# 创建两个三维filter
# ... 大小7*7，通道数由图片决定
# ... 一个水平filter，一个垂直filter（只有某一行或列为1）
filters_test = np.zeros(shape=(7, 7, channels, 2), dtype=np.float32)
filters_test[:, 3, :, 0] = 1 # vertical line
filters_test[3, :, :, 1] = 1 # horizontal line

# 图片占位符
X = tf.placeholder(tf.float32, shape=(None, height, width, channels))
# 添加卷积层
# ... X为输入
# ... filters是所用的一系列filter，列表最后一维是filter的索引
# ... stride是步长，针对输入而言的，比如这里batch、行、列、通道的步长分别为1,2,2,1
# ... padding为填充方式，SAME表示填零，VALID表示不填零（可能会舍弃结尾的部分元素）
convolution = tf.nn.conv2d(X, filters, strides=[1,2,2,1], padding="SAME")

with tf.Session() as sess:
    output = sess.run(convolution, feed_dict={X: dataset})

# 显示第一张图片的第二个feature map
plt.imshow(output[0, :, :, 1])
plt.show()

padding参数，SAME和VALID的区别——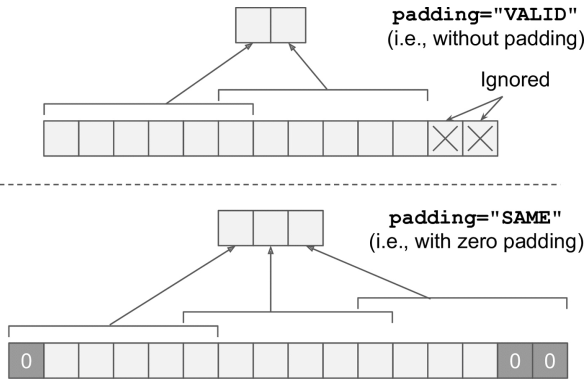
padding

池化层

借助tf.nn.max_pool()、tf.nn.avg_pool() 等——

import numpy as np
from sklearn.datasets import load_sample_images

# 读入一些图片
dataset = np.array(load_sample_images().images, dtype=np.float32)
batch_size, height, width, channels = dataset.shape

# 图片占位符
X = tf.placeholder(tf.float32, shape=(None, height, width, channels))
# 添加最大池化层
# ... X为输入的数据
# ... ksize为池化核大小，这里表示每次一张图片，池化核大小为2x2，池化核每次只应用于一个通道
# ...... 注意：tensorflow不支持多对象池化，所以第一维必须是1
# .......... 而且，只支持平面池化或者深度池化
# .......... 也就是说，要么深度（通道）参数置为1，要么长宽都置为1
# ... stride为步长，同卷积层，这里batch、行、列、通道的步长分别为1,2,2,1
# ... padding为填充方式，同卷积层，这里表示不填充
max_pool = tf.nn.max_pool(X, ksize=[1,2,2,1], strides=[1,2,2,1], padding="VALID")

with tf.Session() as sess:
    output = sess.run(max_pool, feed_dict={X: dataset})

# 显示第一张图片池化后的效果
plt.imshow(output[0].astype(np.uint8))
plt.show()

内存占用计算（以卷积层为例）

考虑 $N_f$ 个大小为 $m_f \times n_f \times c$ 的三维filter组成的卷积层，
假设输入数据（比如图片）大小为 $m_i \times n_i$，每个batch有 $N_i$ 个instances，
那么每个filter输出feature map的大小也为 $m_i \times n_i$；

此时,
该卷积层包含参数数量为——
$$ N_p = (m_f \times n_f \times c \underbrace{+1}_{\text{偏置单元}}) \times N_f $$
该卷积层输出的feature maps的变量总数为——
$$ N_v = m_i \times n_i \times N_i $$
该卷积层每一趟要执行的运算次数为——
$$ N_o = \underbrace{m_i \times n_i \times N_i}_{\text{feature maps的变量总数}} \times \underbrace{m_f \times n_f \times c}_{\text{卷积核大小}} $$

比如，200个大小为 $5 \times 5 \times 3$ 的filter组成的卷积层，输入大小为 $150 \times 100$ 的三通道图片；
那么该层参数数量为 $ (5 \times 5 \times 3 + 1) \times 200 = 15200 $ ；
如果每个batch大小为1，使用float32存储变量，那么需要占用内存 $200 \times 150 \times 100 \times 32 = 96,000,000bits$ （约11.4MB）；
需要进行 $200 \times 150 \times 100 \times 5 \times 5 \times 3 = 225,000,000$ 次float乘法；

解决内存溢出的办法：

加大步长达到降维的目的（使feature map比输入小）
减少一些层
使用占用空间更少的变量类型
分布式运算

经典的CNN分类架构

目前常见的CNN分类架构有LeNet-5、AlexNet(2012)、NIN(2014)、VGG-Nets(2015)、GoogLeNet(2015)、ResNet(2015)等；
详见《经典的CNN分类架构 | Hey~YaHei!》

目标检测架构

参见从RCNN到SSD，这应该是最全的一份目标检测算法盘点 | 机器之心(2018)【原文】

CNN可视化

论文：

Adaptive Deconvolutional Networks for Mid and High Level Feature Learning(2011) 提出反卷积技术
Visualizing and Understanding Convolutional Networks(2013) 用反卷积技术实现CNN可视化（以AlexNet为例）

网络压缩

深度神经网络面临严峻的过参数化（over-parameterization）问题，
如论文 Predicting Parameters in Deep Learning(2014) 指出只给定很小一部分参数子集（约5%）就可以完整地重构剩余的参数；

但事实上，参数的冗余在模型训练过程中是十分必要的，因为面临一个极其复杂的非凸优化问题，对现有基于梯度下降的优化算法而言，参数冗余保证了网络能够收敛到一个比较好的最优值。一定程度上，网络越深，参数越多，模型越复杂，最终效果也往往越好；

压缩既指体积上的压缩，也指时间上的压缩。
绝大多数压缩算法旨在将一个庞大而复杂的预训练模型转化为一个精简的小模型；
按对网络结构的破坏程度分，可以分为前端压缩和后端压缩——

前端压缩
不改变原网络结构，仅仅在原模型基础上减少网络层数或滤波器个数，可以完美适配现有的深度学习库；
主要包括知识蒸馏、紧凑的模型结构设计、滤波器层面的剪枝等
后端压缩
尽可能减少模型大小，对原始网络造成极大程度的改造（往往不可逆），必须开发相应配套的运行库甚至专门的硬件设备；
主要包括低秩近似、未加限制的剪枝、参数量化、二值网络等
前端压缩和后端压缩是互补的关系
通过相互结合，将前端压缩和后端压缩级联起来，可以在最大程度上减少模型复杂度
此外，也有人试图设计更加紧凑的网络结构，对新的网络结构进行训练
这也能减小模型复杂度，但不是严格意义上的网络压缩

数据扩充

有效的数据扩充通过扩充训练样本数量，增加样本多样性，一方面可以避免过拟合，另一方面会给模型性能带来提升；

简单的数据扩充

图像水平翻转
数据集扩充一倍
随机抠取
一般用较大的正方形（0.8~0.9倍的原图大小）在原图的随机位置抠取图像块；
抠取次数决定数据集的扩充倍数；
同时用设定好的比例抠取图像，避免了图像缩放带来的分辨率失真
尺度变换
将原图等比率缩放为原图的0.8、0.9、1.1、1.2、1.3等倍数；
缩放次数决定数据集的扩充倍数；
增加CNN在物体尺度上的鲁棒性
旋转
将原图旋转-30度、-15度、15度、30度等角度；
旋转次数决定数据集的扩充倍数；
增加CNN在方向上的鲁棒性
色彩抖动
在RGB颜色空间对色彩分布进行轻微扰动，在HSV颜色空间对图像饱和度、明度、色调进行轻微扰动；

实践中往往会在上述几种方式叠加使用；
相关实践代码可以参见：aleju/imgaug | github，一个图像数据集的扩充python库

特殊的数据扩充

Fancy PCA
论文：Imagenet Classification with Deep Convolutional Neural Networks(2012)
和AlexNet网络一同提出；
论文指出，Fancy PCA可以近似捕获自然图像的一个重要特性——物体特质与光照强度和颜色变化无关
1. 对整个数据集的R、G、B进行PCA操作，得到特征向量 $p_i$ 和特征值 $\lambda_i$，其中 $i=1,2,3$；
2. 计算一组随机值$[p_1, p_2, p_3][\alpha_1 \lambda_1, \alpha_2 \lambda_2, \alpha_3 \lambda_3]^T$，将其作为扰动加到原像素值中；
  其中，$\alpha_i$ 为0均值0.1标准差的高斯分布随机值
3. 每一个epoch之后，重新选取一次$\alpha_i$进行扰动
监督式数据扩充
海康威视在2016ImageNet竞赛的场景分类任务中提出；
在以物体为中心的图像分类任务中，随机抠取图像块可以取得比较好的效果；
但对于依靠图像整体蕴含的高层语义的场景分类任务中，随机抠取图像块很可能会抠取到关联性比较差的结果（比如“海滩”中抠取到“树”和“天空”）；
可以借助图像标记信息解决这一问题：
1. 根据原数据训练一个分类的初始模型
2. 利用该模型对每张图生成激活图（activation map）或热力图（heat map）
  可以直接将最后一层卷积层特征按深度方向加和得到；
  也可以参照论文 Learning Deep Features for Discriminative Localization 生成分类激活图（class activation map）
  该热力图可以指示图像区域与场景标记之间的相关概率
3. 根据上述概率映射回原图选择较强相关的图像区域作为抠取的图像块

图像预处理：中心式归一化

在训练集上计算各通道的均值，然后对训练集、验证集、测试集上每一个像素点的各通道都减去该均值；
其原理在于，自然图像一般是一类平稳的数据分布，通过减均值操作可以移除图像的共性部分而凸显个体的差异；
比如下图通过减均值操作之后，可以发现背景部分被有效“移除”了，而只保留车、建筑等显著区域
12Image_Preprocess

超参数设定

输入数据像素大小

CNN需要对输入的图像统一大小，通常为了便于GPU设备并行，都会统一将图像压缩为 $2^n$ 大小；
在设备、时间条件允许的情况下，一般分辨率高的数据有助于网络性能的提升，尤其是对基于注意力模型的网络；
一般CNN最后采用FC作为分类器，如果改变了原模型的图像分辨率，通常也需要重新设定FC输入的滤波器大小以及其他相关参数

卷积层参数

包括卷积核大小、卷积步长、卷积核个数（即输出的特征图数量）；

实践中通常采用3x3和5x5的小核，小的卷积核有以下作用：

增加模型复杂度，防止欠拟合
减少参数数量

卷积操作可以选择性的搭配填充操作（padding），有以下作用：

充分利用和处理输入数据的边缘信息
搭配合适的参数可以保持输入、输出大小不变，避免随着网络深度增加输入大小急剧减小
对于fxf的卷积核、步长为1的卷积操作，在边缘各添加 $p=(f-1)/2$ 个像素可以维持输入输出大小不变

为了便于GPU设备方便存储，卷积核个数也即输出的特征图数量通常为 $2^n$ ；

可参考：How can I decide the kernel size, output maps and layers of CNN? | Quora

论文：

Efficient BackProp(1998)
Systematic evaluation of CNN advances on the ImageNet(2017) 比较了ILSVRC上各种技术、模块在不同参数下的表现
对应github评估项目：ducha-aiki/caffenet-benchmark | github

通常，

网络越深越好，但这是以更大的数据集、学习任务复杂度增加为代价的；
batch size设为几百，具体视任务而定，批大小约大计算资源的需求就越高，批大小不宜太小（这会导致估计产生较大的偏差）；
一开始使用较少的特征图数量，然后逐渐增加并且一边观察误差的变化趋势；
小核可以捕捉图像的细节，大核容易丢失图像的细微特征；
可以参考类似任务的网络配置；

池化层参数

池化核一般比较小，如2x2、3x3等
为了不丢弃过多输入而损失网络性能，很少使用超过3x3的池化核
最常用的是2x2大小、2步长的池化操作
此时输出缩小为原来的四分之一，也即丢弃了75%的响应值

训练技巧

随机打乱训练数据：
信息论指出——

从相似的事件中学习总是比从相似事件中学习更具信息量

在每轮（epoch）训练中随机打乱训练数据，使得模型每次在不同批次看到“不同”的数据，
不仅可以提高模型收敛速度，还对模型的泛化性能有略微的提升

学习率设定：

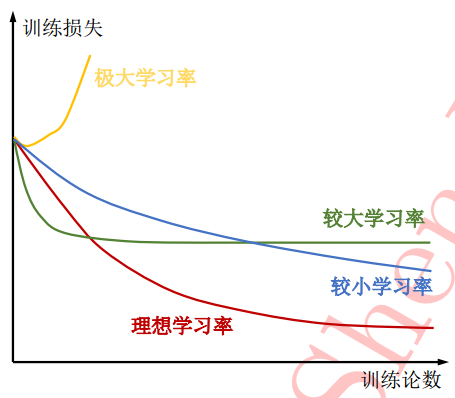
初始学习率不宜过大，以0.01和0.001为宜；
如果刚训练几步模型的loss就急剧上升，说明初始学习率过大
使用一定的学习计划策略
可参见优化器/学习计划 | Hey~YaHei!
训练过程中观察学习曲线（loss随步数的变化）对学习率进行诊断

批规范化操作（BN操作）：
参见梯度消失与梯度爆炸/批量归一化 | Hey~YaHei!

优化器：
参见优化器 | Hey~YaHei!

微调预训练好的神经网络：
用目标任务数据在预训练模型上继续进行训练过程；

网络已经在原始数据上收敛，微调时采用更小的学习率（一般在$10^{-4}$及其以下）
CNN浅层有更强的泛化特征，深层对应更抽象的语义特征；
微调时往往对前层更新的少，对深层更新的多，故可以设置不同的学习率；
微调策略
- 数据较少且任务非常相似时，可仅微调最后的几层
- 数据较多且任务相似时，可以微调更多甚至全部的网络层
- 当数据较少、差异较大时，可以尝试微调，但不一定能成功
  这种情况下还可以借助部分原始数据与目标数据协同训练；
  论文：Borrowing Treasures from the Wealthy: Deep Transfer Learning through Selective Joint Fine-tuning(2017)
  在浅层特征空间选择目标数据的近邻作为协同训练的原始数据子集；
  微调阶段改造为多目标学习任务：将目标任务基于原始数据子集、将目标任务基于全部目标数据；

2018-05-02
将经典的CNN分类架构抽离出来作为单独一篇博文：
《经典的CNN分类架构 | Hey~YaHei!》

2018-05-07
将池化层原理部分抽离出来作为单独一篇博文：
详见《漫谈池化层 | Hey~YaHei!》