3 非线性分类器——神经网络

Author Avatar
YaHei 7月 31, 1995

吴恩达《机器学习》笔记

逻辑回归的局限

Sigmoid函数：$g(z) = \frac{1}{1 + e^{-z}}$
如果只有两个特征：
$$z = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_1 x_2 + \theta_4 x_1^2 x_2 + \theta_5 x_1 x_2^2 + \cdots$$
当特征的数量增加时，参数的个数会快速增长，复杂度为 $O(n^2)$

神经网络的结构

神经元

3-1
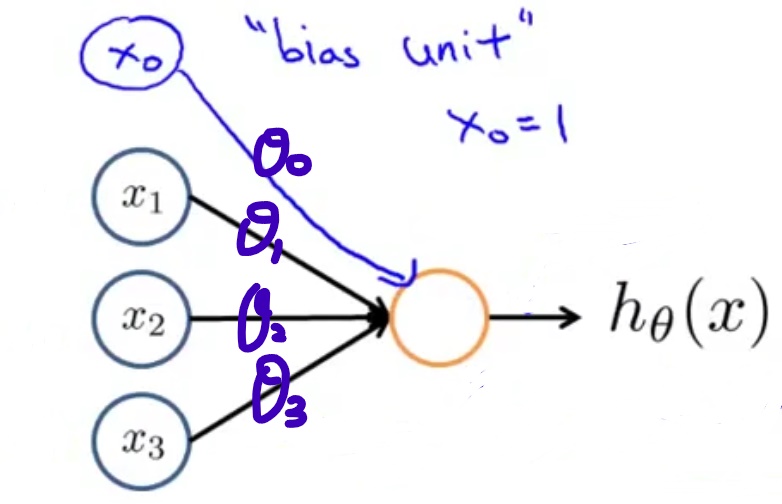
其中橘黄色的圆表示一个神经元，蓝色的圆表示输入，$\theta_0, \theta_1, \theta_2, \theta_3$为权重weights；
$x_0 = 1$ 是偏置单元，一般省略不画出；
$$z = \theta^T x = \theta_0 x_0 + \theta_1 x_1 + \theta_2 x_2 + \theta_3 x_3$$
$$h_\theta(x) = \frac{1}{1+e^{-\theta^T x}}$$

网络

3-2
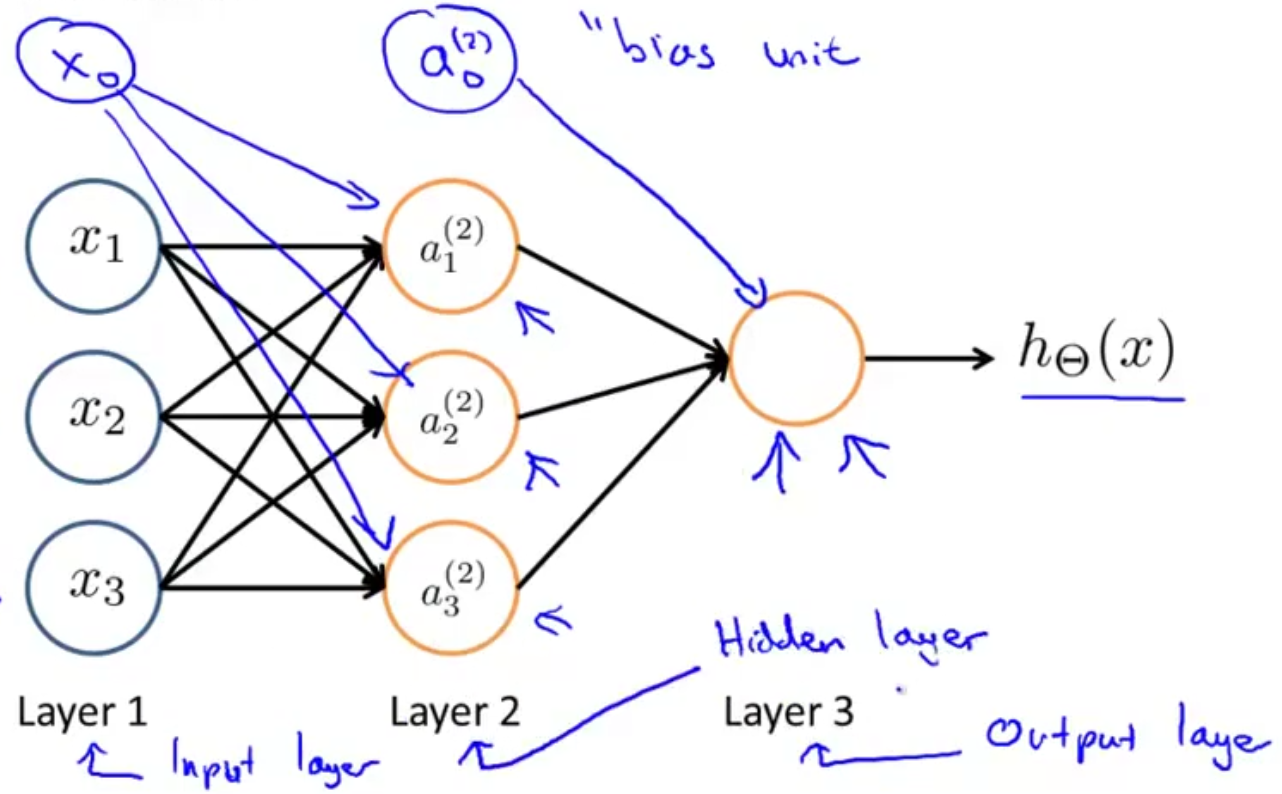
$z_i^{j}$ 表示第j-1层的相关神经元到第j层第i个神经元的输入加权和；
$z^{j}$ 表示第j-1层相关神经元到第j层各神经元的输入加权和构成的行向量；
$a_i^{(j)}$ 表示第j层第i个神经元的激励activation；
$a^{j}$ 表示第j层各个神经元激励构成的行向量；
$\theta_{ij}^{(k)}$ 表示第k层的第i个神经元输出在第k+1层的第j个神经元的权重；
$\Theta^{(k)}$ 表示第k层到第k+1层的权重矩阵；
从左到右前向传播

3-3
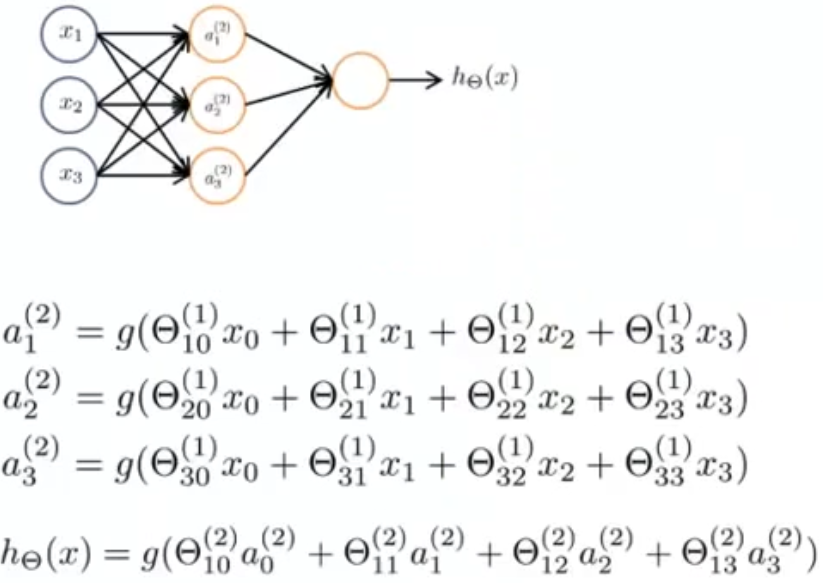
有$a^{(j)} = g(z^{(j)})$，每一层输入都会引入一个偏置单元，且输出层上的神经元的激励即为$h_\Theta(x)$

举例

实现AND逻辑的神经元

3-5
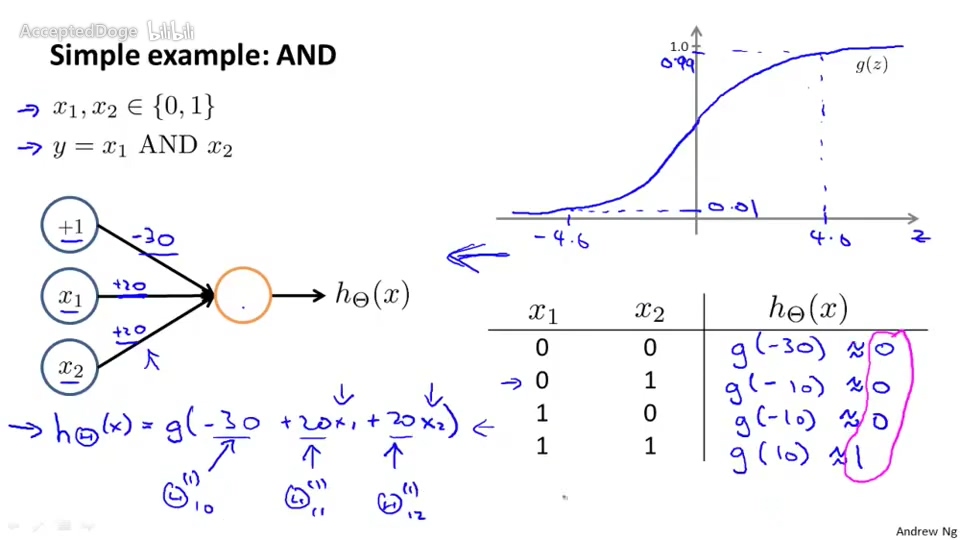
选择适当的权重，即可以实现一个AND逻辑的神经元

实现XNOR逻辑的神经网络

3-4
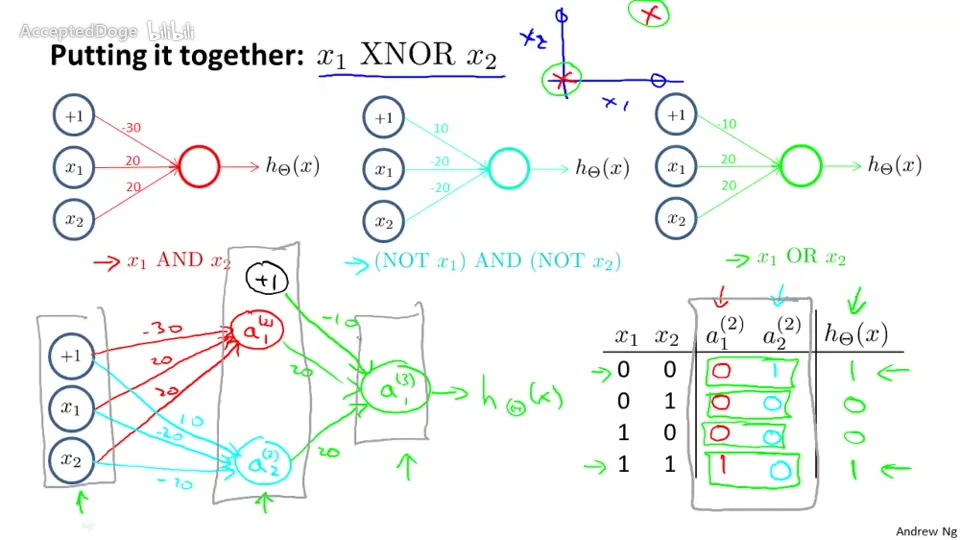
$x_1 XNOR x_2 = [x_1 AND x_2] OR [(NOT x_1) AND (NOT x_2)]$
通过AND逻辑、(NOT) AND (NOT)逻辑、OR逻辑的神经元分层组合即可得到XNOR逻辑的神经网络

反向传播算法

成本函数Cost function

  • 逻辑回归（正则化）
    $$J(\theta) = -\frac{1}{m} \sum_{i=1}^{m}[ y^{(i)} log h_\theta(x^{(i)}) + (1-y^{(i)}) log (1 - h_\theta(x^{(i)})) ] + \frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2$$
  • 神经网络（正则化）
    $$J(\Theta) = -\frac{1}{m}[ \sum_{i=1}^{m} \sum_{k=1}^{K} y_k^{(i)} log( h_\Theta(x^{(i)}) )_k + (1-y_k^{(i)}) log( 1-(h_\Theta(x^{(i)}))_k ) ] + \frac{\lambda}{2m} \sum_{l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_l +1} (\Theta_{ji}^{(l)})^2 $$
    其中，
    网络有K个输出，L层，$s_l$是第l层的神经元数量

操作过程

  1. 令$\Delta_{ij}^{(l)} = 0 （对所有l,i,j）$

  2. for i = 1 to m

    1. 令$a^{(1)} = x^{(i)}$
    2. 前向传播，利用$a^{(1)}$递推计算$a^{(l)} (l=2,3,…,L)$
      $$ z^{(l)} = \Theta^{(l-1)} a^{(l-1)} $$
      $$ a^{(l)} = g(z^{(l)}) $$
    3. 已知$y^{(i)}$，可以计算得到输出层各输出神经元的的误差
      $$ \delta^{(L)} = a^{(L)} - y^{(i)} $$

    4. 反向传播，利用$\delta^{(L)}$递推计算$\delta^{(l)} (l = L-1, L-2, …, 2)$
      $$ \delta^{(l)} = (\Theta^{(l)})^T \delta^{l+1} .* g’(z^{(l)}) $$

      可以推导得到——（推导过程略）
      $$g’(z^{(l)}) = a^{(l)} .* (1-a^{(3)})$$
      不需要计算$\delta^{(1)}$，因为第一层是输入层，没有误差

    5. 分别更新$ \Delta_{ij}^{(l)} $
      $$ \Delta_{ij}^{(l)} := \Delta_{ij}^{(l)} + a_j^{(l)} \delta_i^{(l+1)} $$
      可以写成——
      $$ \Delta^{l} := \Delta^{(l)} + \delta^{(l+1)} (a^{(l)})^T $$
  3. 计算$ D_{ij}^{(l)} $
    $$ D_{ij}^{(l)} := \frac{1}{m} \Delta_{ij}^{(l)} ，若j = 0 $$
    $$ D_{ij}^{(l)} := \frac{1}{m} \Delta_{ij}^{(l)} + \lambda \Theta_{ij}^{(l)} ，若j \neq 0 $$
  4. 可以证明——（证明过程略）
    $$ \frac{\partial}{\partial \Theta_{ij}^{(l)}} J(\Theta) = D_{ij}^{(l)} $$
  5. 最后应用梯度下降算法即可求得$\Theta$

梯度检验

  • 原因
    神经网络模型比较复杂，所以在实现这个模型时可能会出现一些错误；
    导致 $J(\Theta)$ 在减小，但最终的模型误差仍然偏高
  • 近似求导
    • 考虑单一参数 $\theta$
      • 双侧差分（稍微准确些）
        $$ \frac{d}{d \theta} \approx \frac{J(\theta + \epsilon) - J(\theta - \epsilon)}{2 \epsilon} $$
      • 单侧差分
        $$ \frac{d}{d \theta} \approx \frac{J(\theta + \epsilon) - J(\theta)}{2 \epsilon} $$
    • 多参数
      $$ \frac{\partial}{\partial \theta_1} \approx \frac{J(\theta_1 + \epsilon, \theta_2, \theta_3, …) - J(\theta_1 - \epsilon, \theta_2, \theta_3, …)}{2 \epsilon} $$
      ……以此类推
    • $\epsilon$ 取得很小，如 $\epsilon = 10^{-4}$；
      但也不能太小，否则计算机在运算时会出现数值问题
  • 梯度检验
    检验神经网络每次迭代中，近似求导的结果与D是否相近
  • 实际训练时必须关闭梯度检验
    近似求导的计算量要比反向传播大的多；
    只用来检验复杂模型的实现是否正确

实际应用

随机初始化

  • 逻辑回归中可以将参数都初始化为0，但神经网络不行
    若将神经网络的参数都初始化为0，会出现一层中各个神经元的训练结果一致而失去意义
  • 神经网络的参数初始化
    随机初始化参数 $\theta \in [-\epsilon, \epsilon]$ ，$\epsilon$ 很小；
  • 通过随机初始化可以打破数据对称性的影响

标记的表示方式

不能简单地用 $y=1,2,3,4,5, …$ 来表示标记；
而应使用一个 $K \times 1$ 的列向量来表示，其中只有一项为1，其余为0，如
$$y^{(i)} =
\left[ \begin{array}{ccc}
0\\\
0\\\
\vdots\\\
1\\\
\vdots\\\
0\\\
0
\end{array} \right]$$

神经元数量

  • 输入层的神经元数量取决于输入的特征数
  • 输出层的神经元数量取决于分类数
  • 各个隐藏层的神经元数量应相等
    一般来说，隐藏层神经元数量越多网络的效果越好，但计算量也就越大