自编码器

Author Avatar
YaHei 4月 25, 2018


BGM：《末日时在做什么？有没有空？可以来拯救吗？》第九话插入曲
这番名字真是狗血，但剧情和音乐出奇的不错

参考《Hands-On Machine Learning with Scikit-Learn and TensorFlow(2017)》Chap15
《Hands-On Machine Learning with Scikit-Learn and TensorFlow》笔记

自编码器工作方式非常简单，就是学习如何模仿输入来产生输出；
我们会采取各种约束（比如限制输出大小、加噪等）来避免自编码器纯粹地把输入作为输出，从而得到一个高效的数据表示方式；
简而言之，自编码器通过尝试学习某些约束下的特征函数来产生输入的编码，也即一种高效的数据表示；
自编码器可以无监督学习输入数据的编码方式、降低数据维度、作为特征检测器、作为生成模型等等……

数据的高效表示

论文 Perception in chess(1973) 研究了记忆、概念、模式匹配之间的联系；

自编码器可以分为Encoder和Decoder两部分，
Encoder也称识别网络，用于将输入转换为某种内部表示；
Decoder也称生成网络，用于将内部表示转换成输出；
架构跟MLP一样，不过他的输出神经元数与输入数相等，中间层的神经元数小于输入数；
也就是说，中间层的输出必定是输入的一个不完全表示，我们的目的就在于训练出一个输出与输入相近的网络——
可以理解为Encoder是对输入的一个有损压缩，Decoder对其进行解压，我们要训练一个损耗率尽可能小的网络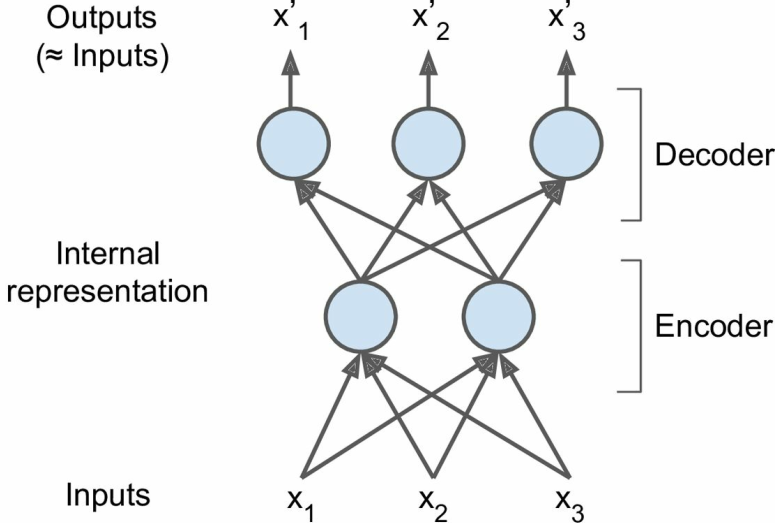
15Simple_Autoencoder

简单的线性自编码器

无非线性激活，MSE损失函数，可以实现一个PCA； 

import tensorflow as tf
from tensorflow.contrib.layers import fully_connected

# 三维输入编码为二维表示
n_inputs = 3
n_hidden = 2
n_outputs = n_inputs

learning_rate = 0.01

X = tf.placeholder(tf.float32, shape=[None, n_inputs])
hidden = fully_connected(X, n_hidden, activation_fn=None)       # 纯线性，无激活
outputs = fully_connected(hidden, n_outputs, activation_fn=None)

reconstruction_loss = tf.reduce_mean(tf.square(outputs - X))    # MSE
optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(reconstruction_loss)

init = tf.global_variables_initializer()

X_train, X_test = [...]     # 载入数据集

n_iterations = 1000
codings = hidden     # 自编码器的目的是获取编码，也即中间层的输出

with tf.Session() as sess:
    init.run()
    for iteration in range(n_iterations):
        training_op.run(feed_dict={X: X_train})     # 无监督
    codings_val = codings.eval(feed_dict={X: X_test})

深层自编码器（Deep autoencoders, or Stacked autoencoders）

深层自编码器为中心对称的“三明治”结构，最中间的一层产生实际的编码，称编码层（Coding Layer），如——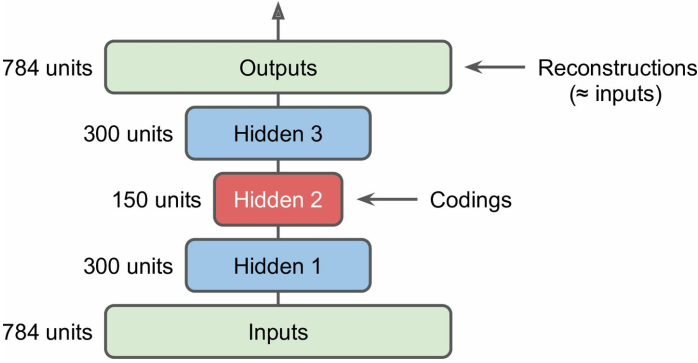
15Stacked_Autoencoder

深度学习的训练技术（如解决梯度爆炸与梯度消失的技术、复用预训练层、优化器、正则化技术等）依旧适用；
与之前讲述的网络的区别在于，自编码器没有标注，是无监督学习

权重共享

由于结构是中心对称的，Encoder和Decoder可以直接共享权重，但tensorflow中的 fully_connected() 没法共享权重，所以需要手动书写全连接层—— 

activation = tf.nn.elu
regularizer = tf.contrib.layers.l2_regularizer(l2_reg)
initializer = tf.contrib.layers.variance_scaling_initializer()

X = tf.placeholder(tf.float32, shape=[None, n_inputs])

weights1_init = initializer([n_inputs, n_hidden1])
weights2_init = initializer([n_hidden1, n_hidden2])

weights1 = tf.Variable(weights1_init, dtype=tf.float32, name="weights1")
weights2 = tf.Variable(weights2_init, dtype=tf.float32, name="weights2")
weights3 = tf.transpose(weights2, name="weights3")      # Decoder，共享Encoder的权重
weights4 = tf.transpose(weights1, name="weights4")      # Decoder，共享Encoder的权重

biases1 = tf.Variable(tf.zeros(n_hidden1), name="biases1")
biases2 = tf.Variable(tf.zeros(n_hidden2), name="biases2")
biases3 = tf.Variable(tf.zeros(n_hidden3), name="biases3")  # Decoder，但偏置还是独立的
biases4 = tf.Variable(tf.zeros(n_outputs), name="biases4")  # Decoder，但偏置还是独立的

hidden1 = activation(tf.matmul(X, weights1) + biases1)
hidden2 = activation(tf.matmul(hidden1, weights2) + biases2)
hidden3 = activation(tf.matmul(hidden2, weights3) + biases3)
outputs = tf.matmul(hidden3, weights4) + biases4

reconstruction_loss = tf.reduce_mean(tf.square(outputs - X))
reg_loss = regularizer(weights1) + regularizer(weights2)    # 只对weights1和weights2施加正则化
loss = reconstruction_loss + reg_loss

optimizer = tf.train.AdamOptimizer(learning_rate)
training_op = optimizer.minimize(loss)

init = tf.global_variables_initializer()

逐层训练

逐层训练然后将各层堆叠起来，要比直接训练一个堆叠好的自编码器要快得多；
比如训练一个三层的自编码器：

  1. 只保留第一隐藏层进行训练
  2. 叠加第二、第三隐藏层进行训练（这里第一隐藏层和第三隐藏层的权重不共享？）
  3. 各层训练完毕，叠加起来得到一个完整的自编码器

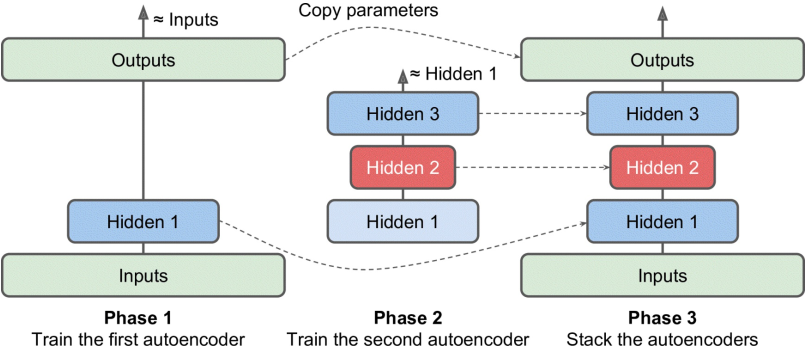
15Training_One_Autoencoder_at_A_Time

可以按照这个描述，分别构造多个计算图来进行训练；
更巧妙的方式是添加一些操作在同一张计算图中区分训练阶段——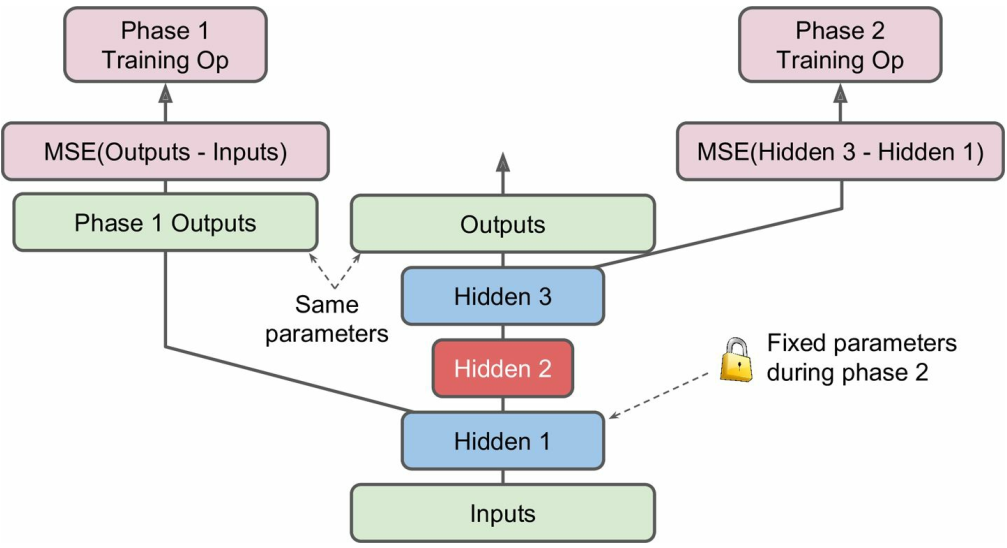
15A_Single_Graph_To_Train_A_Stacked_Autoencoder

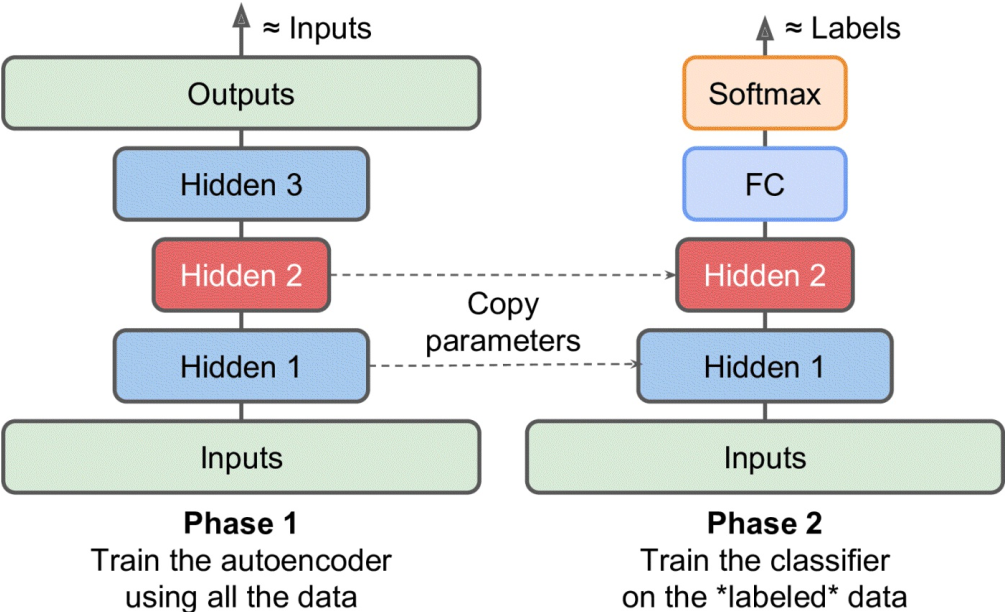
  1. 中间部分是一个完整的自编码器
  2. 左侧是第一训练阶段，旁路了第二和第三隐藏层，Phase 1 Outputs 跟 完整模型中的 Outputs 是共享参数的；
    这一阶段目标是使得最终输出与输入接近，训练 Hidden 1 和 Outputs 的权重
  3. 右侧是第二训练阶段，旁路了输出层，第一隐藏层参数固定，只训练第二和第三隐藏层
    这一阶段目标是使得 Hidden 3 的输出与 Hidden 1 的输出接近，训练 Hidden 2 和 Hidden 3 的权重 
# Build the whole stacked autoencoder normally.
# In this example, the weights are not tied.

# [...] 

optimizer = tf.train.AdamOptimizer(learning_rate)

with tf.name_scope("phase1"):
    # 阶段一的输出层，与完整模型的输出层共享参数
    phase1_outputs = tf.matmul(hidden1, weights4) + biases4

    phase1_reconstruction_loss = tf.reduce_mean(tf.square(phase1_outputs - X))
    phase1_reg_loss = regularizer(weights1) + regularizer(weights4)
    phase1_loss = phase1_reconstruction_loss + phase1_reg_loss

    phase1_training_op = optimizer.minimize(phase1_loss)

with tf.name_scope("phase2"):
    phase2_reconstruction_loss = tf.reduce_mean(tf.square(hidden3 - hidden1))
    phase2_reg_loss = regularizer(weights2) + regularizer(weights3)
    phase2_loss = phase2_reconstruction_loss + phase2_reg_loss

    # 忽略weights1和biases1
    train_vars = [weights2, biases2, weights3, biases3]
    phase2_training_op = optimizer.minimize(phase2_loss, var_list=train_vars)

由于阶段一已经计算了 hidden 1 的输出，而且阶段二中 hidden 1 参数固定；
在内存足够的情况下可以先计算出整个batch上的输出并保留，以减少阶段二的训练时间；
这与复用预训练层 - 复用frozen层输出加速训练类似

重构效果可视化

直接显示压缩再解压后的结果，与输入进行直观的比较进行判断；
可以初步判断重构的效果

特征可视化

对于高层神经元，尤其是最后一个隐藏层的神经元，可以直接观察特定的输入时哪些神经元激活程度比较高；
但底层神经元关注的是更抽象、更小的特征，是我们无法直接理解的特征；

  1. 用权重分布图来观察每一个神经元的关注点
    比如观察第一隐藏层前五个神经元的关注点： 
     with tf.Session() as sess:
     [...] # train autoencoder
     weights1_val = weights1.eval()
 for i in range(5):
     plt.subplot(1, 5, i + 1)
     plot_image(weights1_val.T[i])
    15Visualzing_The_Feature
    【越是关注的像素点，权重越大，在灰度图中就越亮】
    可以看到前四个神经元关注的都是某些局部的小区域，第五个神经元则似乎更关注竖直的笔画
  2. 随机输入一个图像，然后用反向传播不断改变图像以最大化某个神经元的激活程度
    经过一定的迭代次数之后，图像将被扭曲为明显带有该神经元所关注特征的图像
  3. 如果用自编码器用于某些任务（如分类任务）的前期无监督预训练
    那么可以直接通过观察这些任务的最终表现，来判断自编码器的效果

用自编码器作无监督预训练

《Handson-ML》笔记 - 无监督预训练
论文：Greedy Layer-Wise Training of Deep Networks(2006)

15Unsupervised_Pretraining

不同约束下的自编码器

添加约束，避免自编码器纯粹地把输入作为输出，从而得到一个更加高效的数据表示方式

降噪自编码器（Denoising Autoencoders）

论文：
Extracting and Composing Robust Features with Denoising Autoencoders(2008) 提出自编码器可以用于特征提取；
Stacked Denoising Autoencoders: Learning Useful Representations in a Deep Network with a Local Denoising Criterion(2010) 提出降噪自编码器；

降噪自编码器通过对输入加入高斯噪声或者在输入之后紧接一个dropout层，可以有效的避免输入噪声对模型的影响；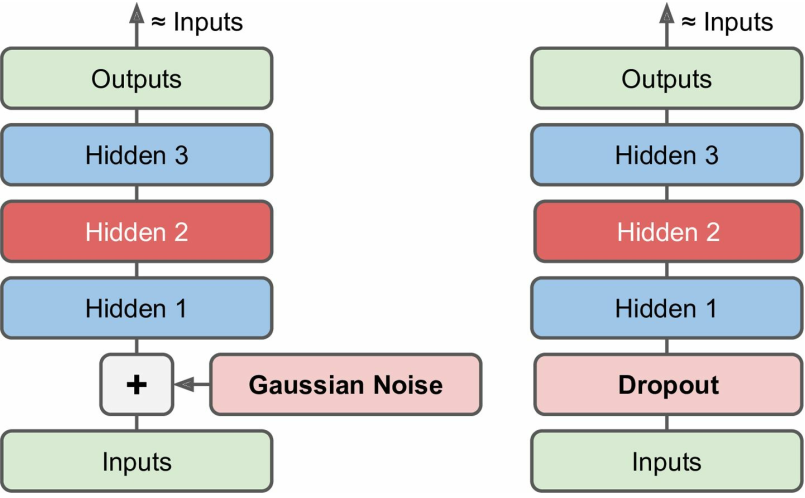
15Denoising_Autoencoders

具体实现：
【高斯噪声方案】 

X = tf.placeholder(tf.float32, shape=[None, n_inputs])
X_noisy = X + tf.random_normal(tf.shape(X))
# [...] 其他层

【dropout层方案】 

keep_prob = 0.7

is_training = tf.placeholder_with_default(False, shape=(), name='is_training')
X = tf.placeholder(tf.float32, shape=[None, n_inputs])
X_drop = dropout(X, keep_prob, is_training=is_training)
# [...] 其他层

稀疏自编码器（Sparse Autoencoders）

基本思想是为损失函数添加适当的稀疏度损失项，使得对于每个输入，编码层只有一小部分神经元被显著激活；
这使得编码器可以更好地提取出特征；
如果只让你用一句话描述自己的想法，那你可能会深思熟虑如何更好的表达

在每次迭代前，都必须先评估编码层的实际稀疏程度——计算编码层中活跃神经元的平均数量；
为了获取比较准确的平均数量，batch的大小一定不能太小；

接下来我们为损失函数添加一个关于神经元活跃程度的惩罚项，比如用MSE；
但更好的方式是用具有更大梯度的KL散度（Kullback–Leibler divergence）；

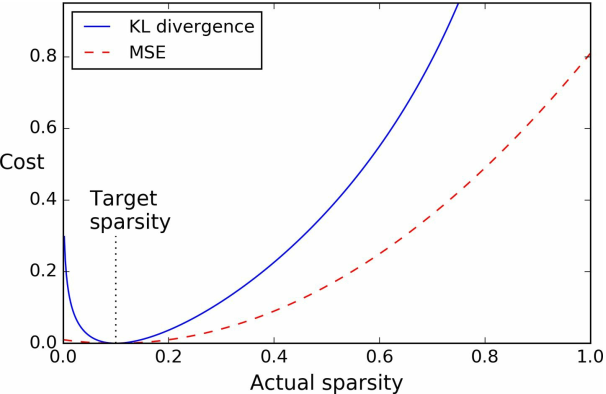
15Sparsity loss

对于两个离散概率分布P和Q，KL散度表示为——
$$ D_{KL}(P||Q) = \sum_i P(i) log \frac{P(i)}{Q(i)} $$

具体到稀疏自编码器上，对于评估的激活概率q和目标激活概率p，KL散度为（激活/不激活 是二项分布的）——
$$ D_{KL}(p||q) = p log \frac{p}{q} + (1-p) log \frac{1-p}{1-q} $$

一旦计算出编码层上每个神经元的稀疏度损失，就可以把他们都加和到损失函数上进行训练；
为了权衡稀疏度损失和重构损失的重要性，可以为加和的稀疏度损失额外添加一个数值合适的权重超参数进行训练；

具体实现： 

# 计算KL散度
def kl_divergence(p, q):
    return p * tf.log(p / q) + (1 - p) * tf.log((1 - p) / (1 - q))

learning_rate = 0.01
sparsity_target = 0.1
sparsity_weight = 0.2

# [...] # Build a normal autoencoder (in this example the coding layer is hidden1)
# 注意：编码层的激活程度必须是在(0,1)区间的
#    比如可以用sigmoid函数强制激活程度归一化为(0,1)区间的数值
#    hidden1 = tf.nn.sigmoid(tf.matmul(X, weights1) + biases1)

optimizer = tf.train.AdamOptimizer(learning_rate)
hidden1_mean = tf.reduce_mean(hidden1, axis=0)         # 计算整个batch上的平均值
sparsity_loss = tf.reduce_sum(kl_divergence(sparsity_target, hidden1_mean))     # 计算稀疏度损失总和
reconstruction_loss = tf.reduce_mean(tf.square(outputs - X))    # 计算重构损失（MSE）
loss = reconstruction_loss + sparsity_weight * sparsity_loss    # 计算全局损失

training_op = optimizer.minimize(loss)

把重构损失 reconstruction_loss 的计算改为交叉熵可以加速收敛，但要注意交叉熵要求输入归一化，因此—— 

logits = tf.matmul(hidden1, weights2) + biases2)
outputs = tf.nn.sigmoid(logits)     # 训练时outputs不是必要的，只是为了看到重构结果才计算outputs
reconstruction_loss = tf.reduce_sum( tf.nn.sigmoid_cross_entropy_with_logits(labels=X, logits=logits) )

变分自编码器（Variational Autoencoders）

论文：Auto-Encoding Variational Bayes(2014)

主要特点：

  1. 概率自编码器，输出是有一定偶然性的，即使是训练完之后
  2. 生成自编码器，能够生成类似他们在训练集上采样的实例

这跟RBMs有些类似，但变分自编码器更加容易训练而且采样更快！

其结构如下所示，编码层不再直接输出编码，而是在 $\mu$ 附近随机采样——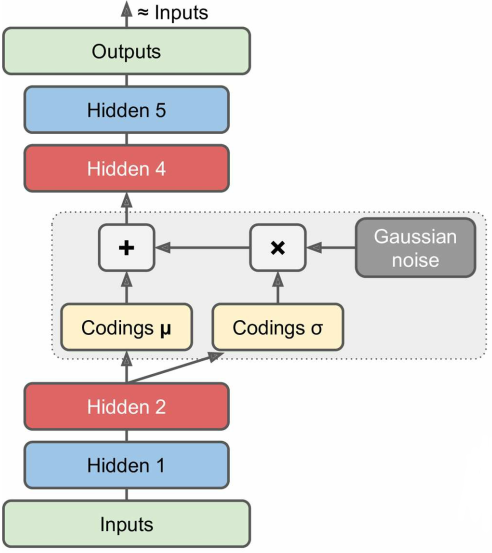
15Variational_Autoencoder

比如下图的输入数据，编码层将在以 $\mu$ 为中心，半径为 $\sigma$ 的范围内随机采样作为编码结果；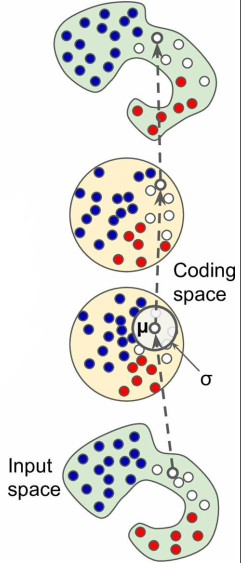
15Variational_Autoencoder_Instance

损失函数分为两个部分：

  1. 重构损失

  2. 隐藏损失：即编码层上的在高斯分布下的损失（这一部分用高斯分布的目标分布和实际分布的KL散度来表示）
    高斯分布的噪声使传输给编码层的信息数量受限，迫使网络学习一些有意义的特征；
    这在数学计算上复杂了不少，不过可以用下列这个式子进行简化——
    $$ L_l = \frac{1}{2} \sum \sigma^2 + \mu^2 - 1 - log(eps + \sigma^2) $$
    通常取 $eps=10^{-10}$，用于防止 $log(0)$ 的情况出现；
    有一种变种的损失函数——
    $$ L_l = \frac{1}{2} \sum e^\gamma + \mu^2 - 1 - \gamma $$
    其中 $\gamma = log(\sigma^2)$，即 $\sigma = e^{\gamma / 2}$；
    该变种使得不同尺度下的 $\sigma$ 更容易被捕获，从而加速收敛； 

     # [...] 超参数

 with tf.contrib.framework.arg_scope(
         [fully_connected],
         activation_fn=tf.nn.elu,
         weights_initializer=tf.contrib.layers.variance_scaling_initializer()):
     # [...] 前层，hidden3为编码层
     hidden3_mean = fully_connected(hidden2, n_hidden3, activation_fn=None)    # 从hidden2习得平均值
     hidden3_gamma = fully_connected(hidden2, n_hidden3, activation_fn=None)   # 从hidden2习得gamma（与标准差相关）
     hidden3_sigma = tf.exp(0.5 * hidden3_gamma)     # 计算标准差sigma
     noise = tf.random_normal(tf.shape(hidden3_sigma), dtype=tf.float32)     # 高斯分布噪声
     hidden3 = hidden3_mean + hidden3_sigma * noise  # 在以平均值为中心，标准差为半径的范围内随机采样
     # [...] 后层
     logits = fully_connected(hidden5, n_outputs, activation_fn=None)    # 用于计算损失函数
     outputs = tf.sigmoid(logits)        # 实际输出

 # 计算重构损失
 reconstruction_loss = tf.reduce_sum(
                         tf.nn.sigmoid_cross_entropy_with_logits(labels=X, logits=logits))
 # 计算隐藏损失
 latent_loss = 0.5 * tf.reduce_sum(
                         tf.exp(hidden3_gamma) + tf.square(hidden3_mean) - 1 - hidden3_gamma)
 # 计算全局损失
 cost = reconstruction_loss + latent_loss

 # [...] 优化器等训练过程略

其他自编码器