漫谈卷积层
去年刚入手深度学习的时候写过一篇《卷积神经网络CNN | Hey~YaHei!》,简单介绍过卷积层——不过经过一年的学习和实践,对卷积又有了新的认识,原本讲道理应该直接更新修改去年的那篇博文的。但是那篇博文涉及面较广,不单单讲卷积,而且之后还写过几篇引用了那篇博文的内容,拾起来魔改似乎会打乱博客的结构,想想还是新开一篇,希望各位看官别嫌弃我炒冷饭。
本文要点:
- 提出卷积层的背景;
- 标准卷积的过程和原理;
- 标准卷积的计算原理(im2);
- 高效卷积:分组卷积、深度向分解卷积、点向卷积;
- 其他卷积的变种:空洞卷积和变形卷积
背景
参考:《Hands-On Machine Learning with Scikit-Learn and TensorFlow》Chap13
卷积的起源有点仿生的味道,这基于生理心理学上的研究,人在感知视觉的时候具有
- 层次性,底层的视神经往往能感知简单的图像结构,随着层次的提高,高层的视神经可以感知到更加抽象的图形结构最后乃至图形的概念。举个栗子,最底层的视神经能够感知简单的点,随着层次的提高,逐渐能感受线、简单的线段组合、乃至有概念的图像如鱼、房子等;
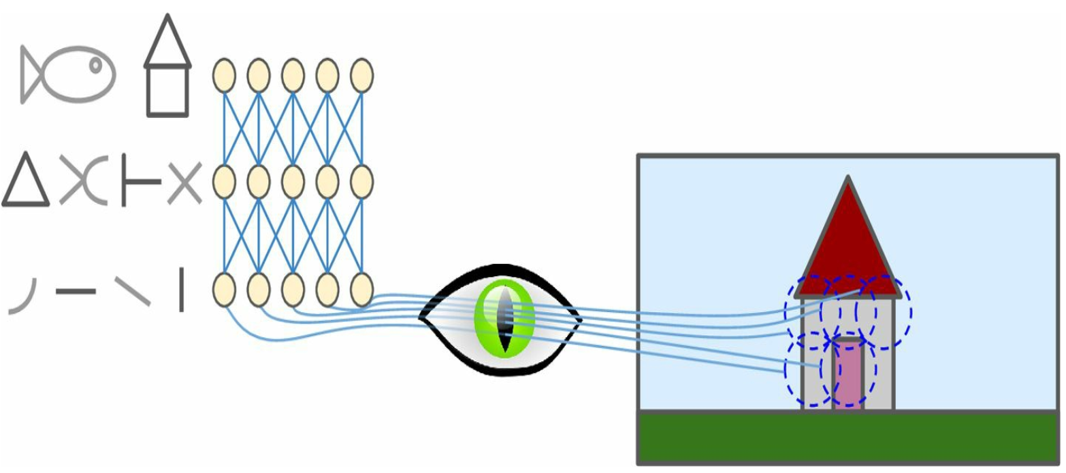
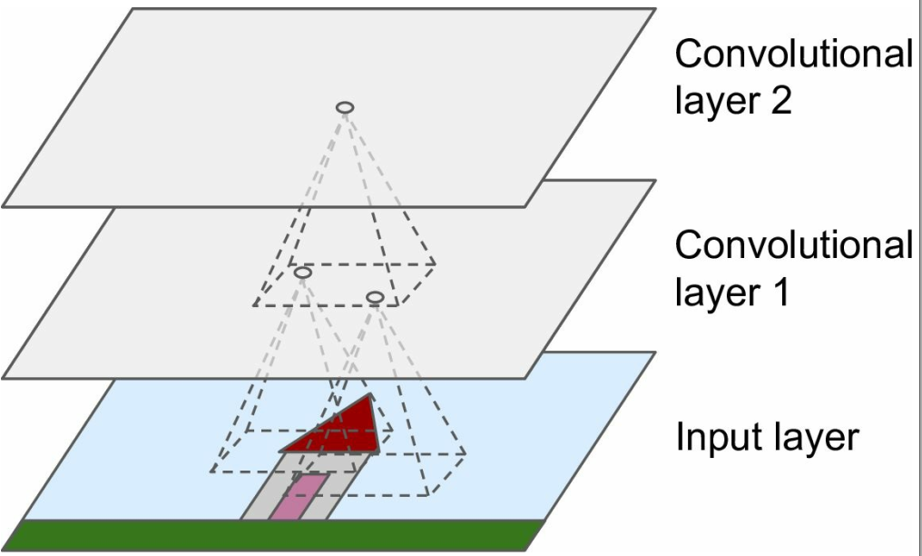
- 局部性,视神经具备有限的感受野,能够将注意力集中的视觉上的局部区域,感受野随着神经网络的深入逐步扩大;
标准卷积(Standard Convolution)
参考:
过程和原理
卷积层并不是使用严格数学意义的卷积运算,而是使用保留卷积性质但抛弃可交换性的互相关函数;
卷积运算具有可交换性,这在数学证明上是很有用的,但在神经网络的应用中却是一个比较鸡肋的性质
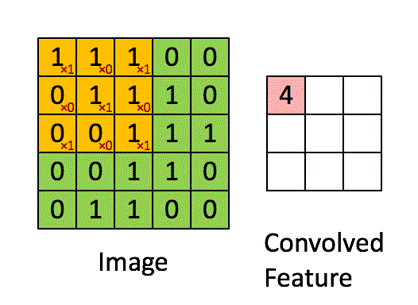
卷积操作选用一定大小的卷积核(下图黄色区域)在原始数据上移动,与重合部分数据做乘和运算;
依次类推,最终输出一张特征图(Feature Map)
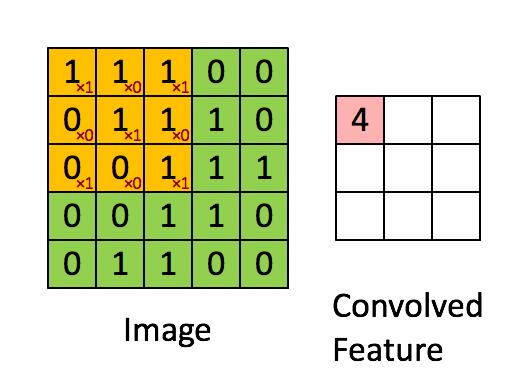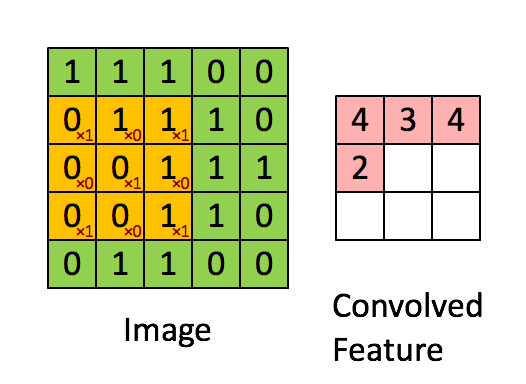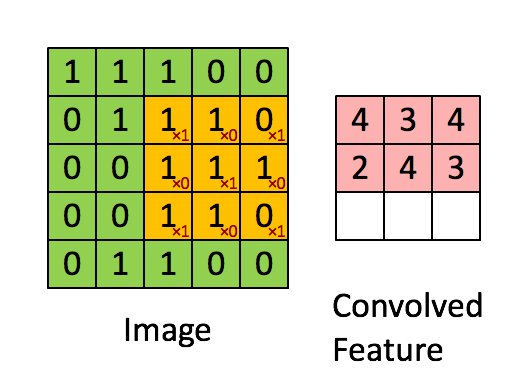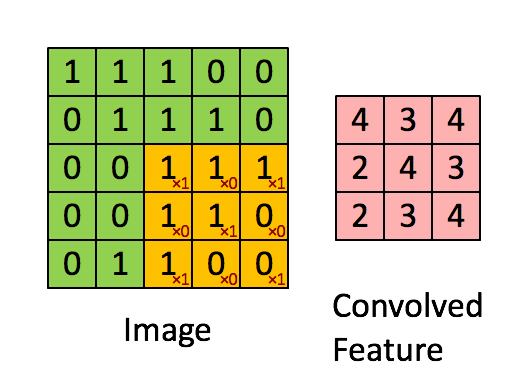
卷积核的作用相当一个滤波器,其参数是经过学习得到的,可以用于提取图片中的特征;
由于核参数是随机初始化的,所以它们很可能会提取出不同的特征;
由低层的卷积层提取简单特征,然后逐层堆叠卷积层,将简单特征逐渐抽象为更高层次的语义概念;
参数和计算量
首先考虑一个单通道输入输出,输出图大小为 $m_o \times n_o$,核大小为 $k_m \times k_n$,带偏置,步长1,不补零的卷积,
$$
\begin{aligned} O _ { 11 } = & w _ { 11 } I _ { 11 } + w _ { 12 } I _ { 12 } + w _ { 13 } I _ { 13 } + \\ & w _ { 21 } I _ { 21 } + w _ { 22 } I _ { 22 } + w _ { 23 } I _ { 23 } + \\ & w _ { 31 } I _ { 31 } + w _ { 32 } I _ { 32 } + w _ { 33 } I _ { 33 } + b \end{aligned}
$$
其参数数量为 $k_m \times k_n + 1$,乘加次数为 $m_o \times n_o \times k_m \times k_n$。
推广到$c_i$通道输入,$c_o$通道输出的情况,
其参数数量为 $(k_m \times k_n + 1) \times c_i \times c_o$,乘加次数为 $m_o \times n_o \times k_m \times k_n \times c_i \times c_o$。
卷积核大小
通常来说,大核卷积可以被多层小核卷积所替代;
比如用三层3x3卷积核的卷积层可以提取到一层7x7卷积核的卷积层一样的特征——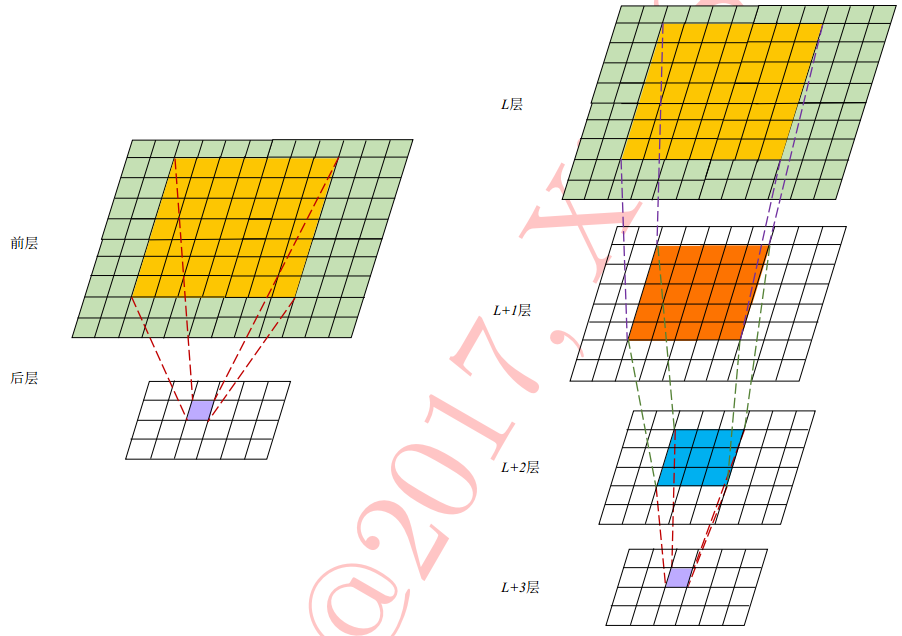
而且,使用多层小核卷积层由以下优势:
- 减少参数
7x7卷积核有 $7 \times 7 = 49$ 个参数,而三层3x3卷积核只有 $3 \times 3 \times 3 = 27$ 个参数 - 增加网络深度
增加网络容量和复杂度
博文《深度学习小技巧(二):模型微调 - 改进2:拆解大核卷积 | Hey~YaHei!》也曾介绍过,改进版的Inception和ResNet目前都已经将7x7卷积层替换成了三层3x3卷积层的堆叠,这里就不再赘述。
长期以来,手工设计的网络都倾向于使用3x3这种小核卷积,但近期随着网络架构搜索的兴起,计算机越来越倾向于使用大核卷积(5x7、7x7乃至9x9和11x11),目前先进的特征提取器几乎不会单纯地使用3x3和1x1的小核卷积。
卷积的计算原理
参考:《深度学习小技巧(二):模型微调 - 高效的1x1卷积 | Hey~YaHei!》
卷积的计算方式可以分为两种——一是直接按照原理计算,二是采用im2col技术进行矩阵乘法;
直接卷积的潜在问题
直接卷积非常直观易懂,但它对目前流行的计算设备来说极其不友好。
首先考虑3x3的单通道特征图,以及k2s1的卷积核——
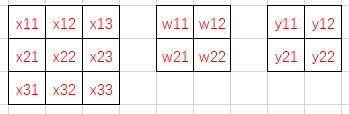
按照卷积计算,
$$y_{11} = w_{11}x_{11} + w_{12}x_{12} + w_{21}x_{21} + w_{22}x_{22}$$
$$y_{12} = w_{11}x_{12} + w_{12}x_{13} + w_{21}x_{22} + w_{22}x_{23}$$
$$y_{21} = w_{11}x_{21} + w_{12}x_{22} + w_{21}x_{31} + w_{22}x_{32}$$
$$y_{22} = w_{11}x_{22} + w_{12}x_{23} + w_{21}x_{32} + w_{22}x_{33}$$
按照“行先序”,特征图和卷积核在内存中是这样排列的——
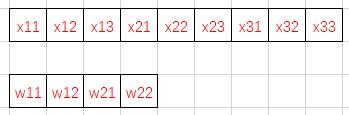
我们用不同的颜色标注出卷积计算中的访存过程(相同颜色的数据相乘)——
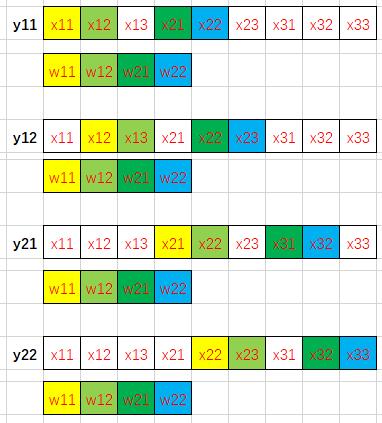
众所周知,由于程序的局部性原理(通常相邻代码段会访问相邻的内存块),现代处理器通常会按块从内存中读取数据到高速缓存中以缓解访存速度和计算速度的巨大差异导致的“内存墙”问题。换句话说,如果计算需要从内存中读取x12的数据,那么往往相邻的x11、x13等数据也会被一起读取到高速缓存上,当下次计算需要用到x11或x13时处理器就可以快速地从高速缓存中取出数据而不需要从内存中调取,大大提高了程序的速度。
注:L1缓存的读取速度是RAM的50-100倍!(数据来源:《计算机体系结构:量化研究方法》)
而从上边展示出来的访存过程中可以看到,直接对于特征图数据的访问过程十分散乱,直接用行先序存储的特征图参与计算是非常愚蠢的选择。
im2col
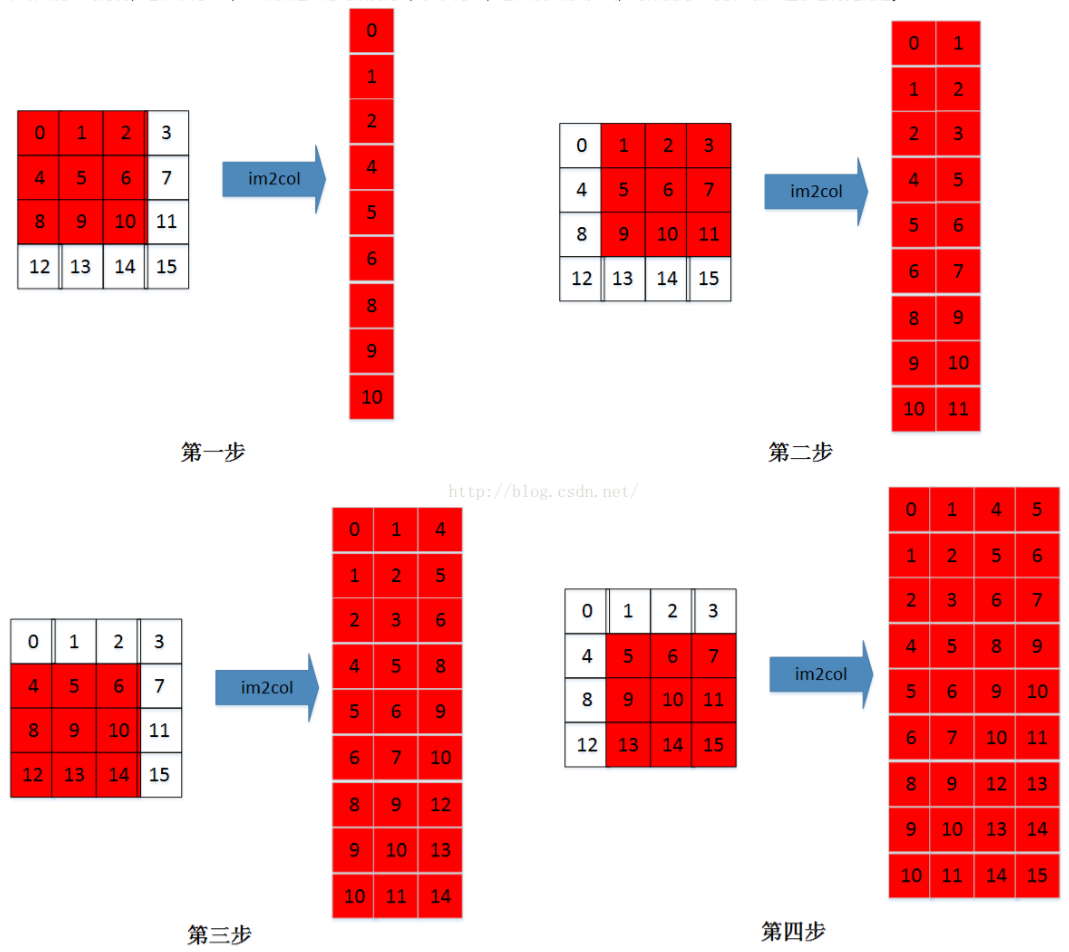
其实思路非常简单:把每一次循环所需要的数据都排列成列向量,然后逐一堆叠起来形成矩阵(按通道顺序在列方向上拼接矩阵)。
比如$C_i \times W_i \times H_i$大小的输入特征图,$K \times K$大小的卷积核,输出大小为$C_o \times W_o \times H_o$,
输入特征图将按需求被转换成$(K*K)\times(C_i*W_o*H_o)$的矩阵,卷积核将被转换成$C_o\times(K*K)$的矩阵,调用GEMM库两矩阵相乘也就完成了所谓的卷积计算。由于按照计算需求排布了数据顺序,每次计算过程中总是能够依次访问特征图数据,迎合了局部性原理,极大地提高了计算卷积的速度!
我用NDArry(MXNet提供的一个类似numpy的数学计算库)实现了一个基于im2col卷积层,除了支持基本的标准卷积外,还支持分组卷积以及量化卷积的模拟运算(int8权重、uint8输入、int32的累积)——
实现代码:Quantization.MXNet/nn/quantized_conv.py#L13 | github, hey-yahei
测试代码:Quantization.MXNet/tests/test_quantized_conv.py | github, hey-yahei
不过要注意的是,im2col也不一定就比直接卷积好!!
- 首先,im2col需要额外的数据重组过程,当一个卷积层非常小(主要是通道比较窄)的时候,直接卷积反而可能会比im2col快(尽管现代网络一般都会用比较宽的通道);
- im2col在重组数据的时候需要对数据产生大量的副本(约 $K^2$ 倍的内存占用);
- 当采用1x1卷积的时候,im2col和直接卷积的过程其实是等价的;
- im2col的目的是迎合程序局部性原理,如果使用了定制化的硬件(比如用FPGA直接实现3x3的卷积运算单元),那么im2col就失去了意义而且反而增加了开销
卷积实现的方式还有很多,这里暂且只介绍im2col,之后有空会独立开一篇文章细谈——
《Winograd卷积原理 | Hey~YaHei!》
高效卷积
早在去年的《MobileNets v1模型解析 | Hey~YaHei!》一文中,我们就分解了标准卷积的工作方式——
将普通卷积的过程分解为“滤波”和“组合”两个阶段——
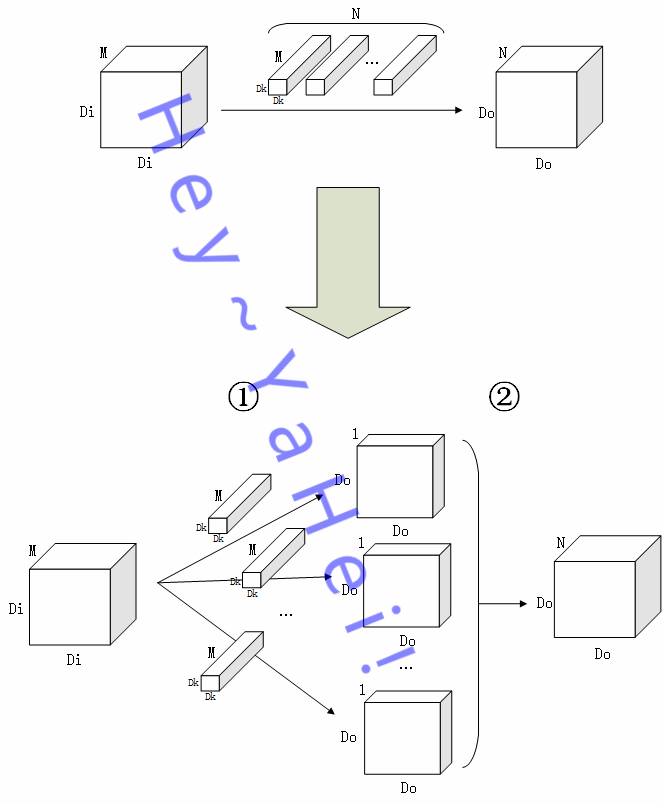
如上图,
假设 $M$ 通道输入图 $I$ 大小为 $D_I \times D_I$,经过一个核大小 $D_K \times D_K$ 的卷积层,最终输出一张大小为 $D_O \times D_O$ 的 $N$ 特征图 $O$
- ①阶段为“滤波”阶段,$N$ 个卷积核分别作用在图 $I$ 的每个通道上提取特征,最终输出 $N$ 张大小为 $D_O \times D_O$ 的单通道特征图;
- ②阶段为“组合”阶段,$N$ 张特征图堆叠组合起来,得到一张 $N$ 通道的特征图 $O$
更详细地,①过程还能进一步分解——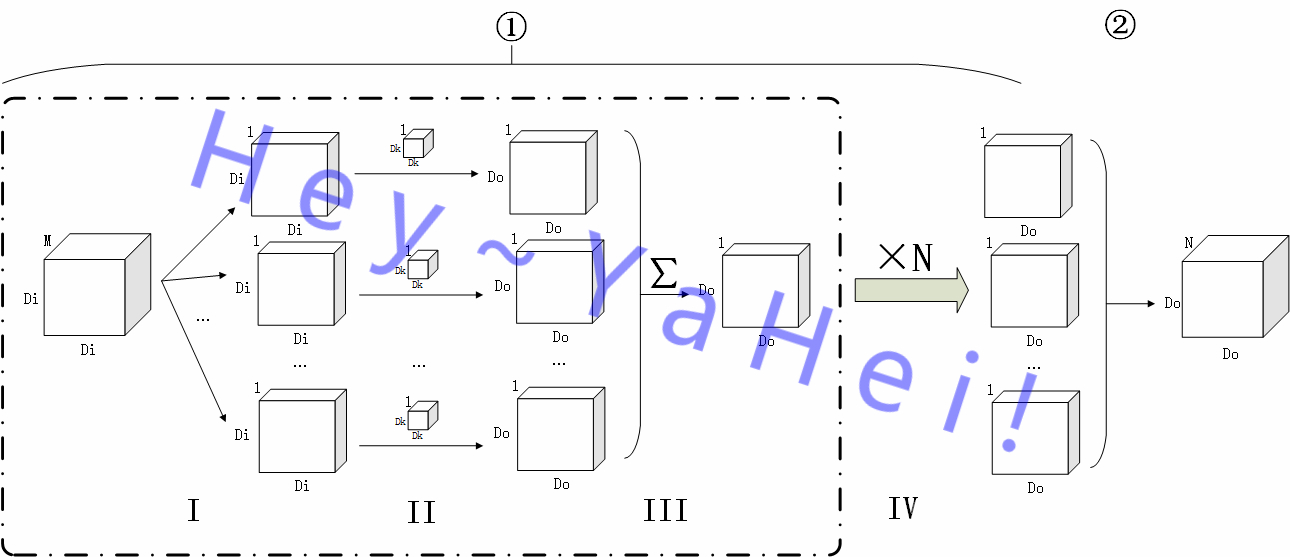
如上图,将①阶段进一步细分为 Ⅰ 到 Ⅳ 四个子阶段,
- Ⅰ 阶段,将原图 $I$ 按通道分离成 $\{ I_1, I_2, …, I_M \}$ 的 $M$ 张单通道图;
- Ⅱ 阶段,用M个卷积核 $K_m$ 对各个单通道图提取特征,分别得到一张大小为 $D_O \times D_O$ 的单通道特征图;
- Ⅲ 阶段,对 Ⅱ 阶段输出的 $M$ 张单通道特征图按通道堆叠起来然后“拍扁”(沿通道方向作加法操作),得到原图在该卷积核作用下的最终输出 $O_n$;
- Ⅳ 阶段,用另外 $N-1$ 个卷积核重复 Ⅱ 、 Ⅲ 阶段,得到 $N$ 张大小为 $D_O \times D_O$ 的单通道特征图
其中 Ⅲ 阶段野蛮地将 $M$ 张特征图拍扁成一张特征图,似乎显得不那么优雅且存在大量的冗余,于是开始有人研究如何让卷积过程变得高效,就出现了分组卷积和深度向分解卷积。
分组卷积(Groupwise Convolution)
分组卷积最初是《ImageNet Classification with Deep Convolutional Neural Networks(2012)》提出,作者最初是出于并行目的(作者有三张仅3G显存的GTX580)把网络拆解到多张显卡上进行训练。顾名思义,分组卷积是对输入通道进行分组,分别施加卷积,最后将卷积结果堆叠起来——也可以理解为将原来的一层卷积等分成若干并行的支路,最后再堆叠汇合。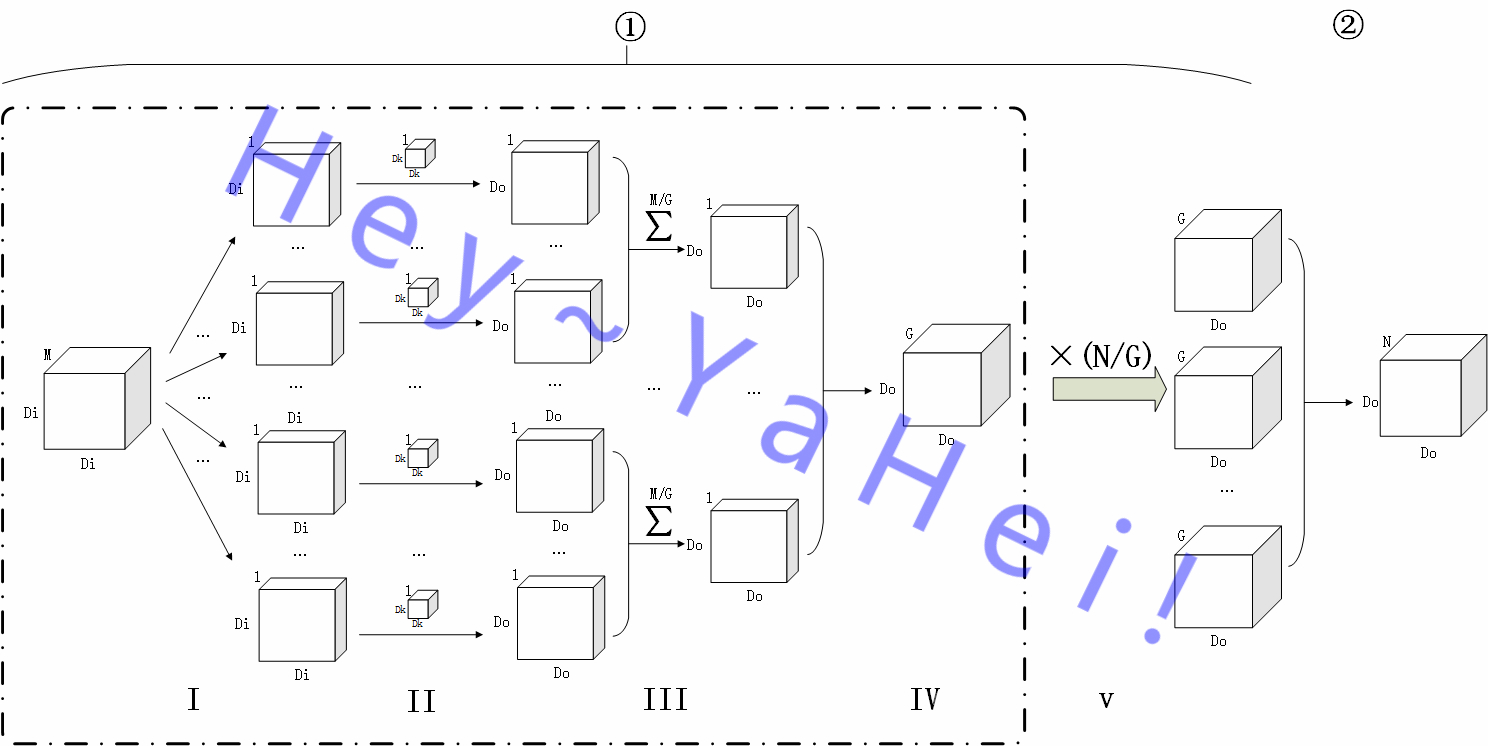
如图所示,传统卷积的 Ⅲ 被拆解成两部分(分组卷积示意图中的Ⅲ和Ⅳ),不再简单的拍扁成一张特征图,而是分成G组分别拍扁,最后堆叠得到G张特征图。这样做有两个好处:
- 传统卷积中Ⅲ阶段的输入包含Ⅱ阶段的所有输出,而分组卷积Ⅲ阶段被分割为G组,每组的输入都是独立的——简而言之,Ⅲ阶段可以分散到多个不同的计算设备上完成而不需要频繁的通信(最终Ⅳ阶段再汇总到主设备上,甚至可以暂存在不同设备上,数据汇总推迟到Ⅴ阶段)
不过目前主流框架似乎没有针对分组卷积做充分的优化,而是简单地对输入、卷积核分组,然后逐一使用标准卷积来实现;一般使用分组卷积的时候也就分个两三组,问题倒是不大,不过到了把分组做到极致的深度向卷积,这个问题就凸显出来,在GPU上专门优化过的深度向卷积要比用分组方式实现的卷积快10倍左右,而CPU并行能力有限,这一问题并不明显,这一点早前已经在《基于MobileNet-SSD的目标检测Demo(一) | Hey~YaHei!》一文中有所提及。 - 参数数量和乘加次数均下降为标准卷积的1/G
简单的实现方法可以参考我的 Quantization.MXNet/nn/quantized_conv.py#L57 | github, hey-yahei。
深度向卷积分解(Depthwise Separable Convolution)
标准卷积同时聚合了所有通道信息和所有空间信息,分组卷积则同时聚合了所有通道信息和部分空间信息,深度向卷积分解直接割裂了通道信息和空间信息的聚合过程,从形式上看则将标准卷积分解为一次深度向卷积和一次点向卷积——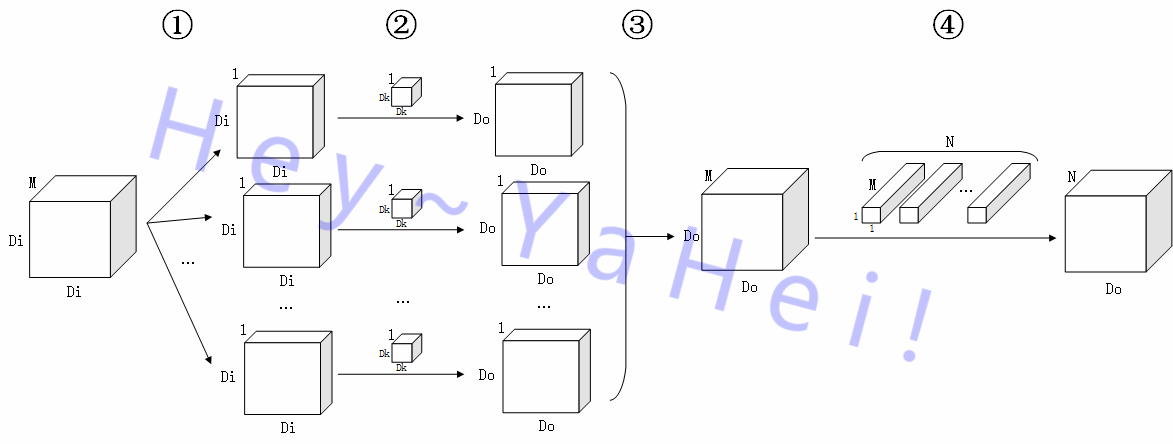
- 滤波Depthwise Convolution
这一过程又称为深度向卷积(Depthwise Convoluon),是分组卷积的一种特例(每个通道作为一组);
①、②阶段与标准卷积①阶段的前两个阶段完全相同,③阶段比标准卷积①阶段的第三个阶段少了一个“拍扁”的过程,直接堆叠形成一张 $M$ 通道的特征图; - 组合Pointwise Convolution
这一过程称又称为点向卷积(Pointwise Convolution);
④阶段用 $N$ 个 $1 \times 1$ 卷积核将特征图从 $M$ 维空间线性映射到 $N$ 维空间上
此时参数数量和乘加次数均下降为标准卷积的 $\frac{1}{D_K^2} + \frac{1}{N}$,不仅如此,由于深度向卷积分解中有 $\frac{N}{D_K^2 +N}$ 的乘加计算集中在1x1卷积上,而通常 $N>>D_K^2$ 也即绝大多数乘加计算由1x1卷积贡献(比如Mobilenet中有94.86%的乘加计算集中在1x1卷积上),所以其计算效率是非常高的。
深度向分解卷积也出现了一些有意思的变种,比如混合感受野的MixConv。
*异构卷积(HetConv)
论文:《HetConv: Heterogeneous Kernel-Based Convolutions for Deep CNNs(2019)》
印度三哥提出来的一种卷积形式,论文里的实验结果非常可观,但似乎没啥影响力(有人说三哥论文数据爱造假?),作者没有开源也没见人复现过,姑且再放着看看吧。
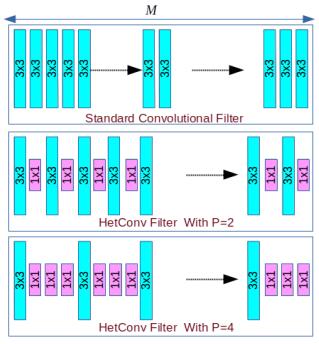
思路倒也简单,有点不定长数组的味道。
应用
高效卷积具有较强的特征提取效率、较高的并行能力,基于这些特点,高效卷积通常被应用于两种场合:
- 注重速度,搭建参数数量、乘加次数均比较少的网络,如MobileNet等;
- 注重性能,用高效卷积替代标准卷积的同时扩张卷积的数量(直到接近标准卷积的规模),如Xception、ResNeXt等
其他卷积变种
空洞卷积
论文:《Multi-scale Context Aggregation by Dilated Convolutions(2015)》
为卷积核增加空洞来扩大感受野,比如
- 3x3的卷积,增加1的空洞,可以在不增加参数数量和运算量的情况下,取得等同5x5卷积的感受野;
- 同理,3x3的卷积,增加2的空洞,可以取得等同7x7卷积的感受野
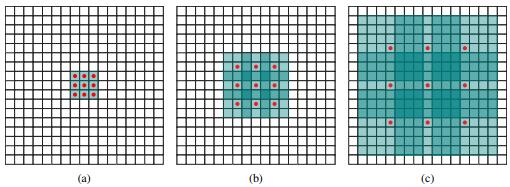
简而言之,就是通过牺牲卷积的“分辨率”,来获取更大的“视野”;
原理很简单,却很有效,目前广泛应用在语义分割领域。
变形卷积
论文:《Deformable Convolutional Networks(2017)》
这两年特别火的一种卷积,利用一个辅助的标准卷积根据input拟合出offset,然后根据offset在input上进行带偏移的采样,最后施加卷积运算——与名字不同,并不是对卷积核进行变形,而是对采样点进行偏移。
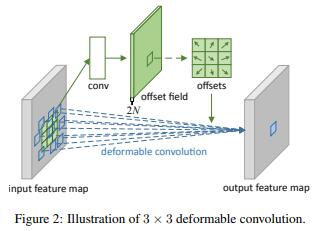
这种卷积广泛存在于各种目标检测、语义分割比赛的冠军方案中。