深度学习小技巧（一）：高效训练

Author Avatar
YaHei 2月 23, 2019

最近无意在MXNet论坛上翻出一篇不错的综述性（实验性）论文《Bag of Tricks for Image Classification with Convolutional Neural Networks(2018)》，作者主要从高效训练、模型微调、训练技巧三个方面列举了一些常见的深度学习小技巧并附上了丰富的比较实验。
之后我将抽空按照这三个方面，以该论文为起点，配以相关的资料和个人理解，连更三篇相关的博文(*^__^*)

数据增强

  • 训练
    • 随机抽样并将uint8转换为float32
    • 随机裁剪出比例尺在$[\frac{3}{4}, \frac{4}{3}]$之间、尺寸大小在$[8\%, 100\%]$之间的图像块，并resize为224x224的图像
    • 以0.5的概率水平翻转
    • 随机使用$[0.6, 1.4]$的系数对亮度、饱和度、对比度进行扰动
    • 用正态分布$\mathcal { N } ( 0,0.1 )$的随机系数为图像添加PCA噪声
    • 图像数值去均值，除以方差
  • 预测
    • 保持比例尺，将短边缩放到256
    • 从中央裁剪出224x224的图像
    • 与训练减去相同的均值，除以相同的方差

高效训练

为了提高训练效率（偶尔训练结果甚至还能有一些微小的提升），目前主流的技巧包括增大训练批次、降低训练精度两个方向，其主要目的在于减少复杂度和提高并行度。

大批次训练

参考：《Don’t Decay the Learning Rate, Increase the Batch Size(2017)》

我们往往直观地认为，加大批次能够让模型在同一次迭代中见识更多的样本，能使得学习更加稳定并取得更好的效果（比如最极端的批梯度下降法），但近年来的各种实验研究表明事实并非如此——在相同学习率、相同epoch下，过大的批大小训练效果反而会比较小的批大小训练结果更差。一般研究认为，这是因为随着批次的增加，样本整体噪声均值不变但方差却被减小，而多数研究认为样本的噪声有助于SGD规避局部最优点（避开尖锐的最优点，提高整体的泛化能力）。论文《On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima(2016)》将这一现象称为“泛化差距（generalization gap）”并展开了详细的讨论。同时论文《A bayesian perspective on generalization and stochastic gradient descent(2017)》经过一系列实验还指出一个经验关系——$B _ { \text {opt} } \propto \epsilon N$，也即最佳的批大小 $B_{opt}$ 随着学习率 $\epsilon$ 和数据集样本总数 $N$ 的乘积等比例增大（缩小）。

随机梯度下降（SGD）

《吴恩达《机器学习》笔记 - 1绪论、线性回归与逻辑回归 - 梯度下降（gradient descent）算法 | Hey~YaHei》已经讨论过梯度下降法，这是机器学习中常用的基本优化方法。传统的梯度下降法的更新方式分为两种，分别是批梯度下降（即每次循环先计算整个数据集上的损失，然后统一更新权重）和增量梯度下降（又称随机梯度下降，每次循环只计算一个数据样本的损失，频繁地更新权重）。前者收敛缓慢，后者受噪声影响大难以收敛到一个很好的最优点。
如今大家常说的“随机梯度下降（SGD）”其实指的是小批次随机梯度下降，该方法介于批梯度下降和增量梯度下降之间，每次循环用若干个样本（数量往往远小于数据集总样本数）的损失来更新权重。

学习率衰减

一般认为，要达到强凸函数的最小点需要在搜索过程中不断衰减学习率，比如论文《A stochastic approximation method(1951)》提出学习率应当满足的收敛条件：
（前提：批大小batch_size固定）
$$\sum _ { i = 1 } ^ { \infty } \epsilon _ { i } = \infty$$
$$\sum _ { i = 1 } ^ { \infty } \epsilon _ { i } ^ { 2 } < \infty$$
其中，$\epsilon_i$ 为第i次更新权重所使用的学习率。

  • 前者保证了经过无穷次更新，无论权重如何初始化，最终都能更新到任意点；
  • 后者要求有足够的学习率衰减速率，使得模型能够收敛到最优点而不是在最优点附近反复震荡

注意上述两式是以批大小固定为前提进行讨论的，而《A Bayesian Perspective on Generalization and Stochastic Gradient Descent(2017)》引入变化的批大小这一因素，重新思考了SGD的收敛条件：
对于梯度下降的更新公式 $\omega_t = \omega_{t-1} - \epsilon \frac{dC}{d\omega_{t-1}}$，从连续时间的角度上看可以得到
$$\frac { d \omega } { d t } = - \epsilon \frac { d C } { d \omega } + \eta ( t )$$
其中，C为无噪声的损失，$\eta(t)$是一个高斯分布的随机噪声，同时论文中将其建模为 $mean(\eta(t))=0$、$variance(\eta(t))=gF(\omega)\delta(t-t’)$ 的高斯随机噪声，其中$F(\omega)$是权重间梯度波动的协方差，$g=\epsilon(\frac{N}{B}-1)$描述了噪声的波动范围，N、B分别是数据集大小和批大小。
通常来说$B << N$，所以有$g \approx \epsilon \frac{N}{B}$；由此可见，在满足$B<<N$的前提下等比例放大（缩小）$\epsilon$和$B$效果是相当的。

学习率衰减实际是一种模拟退火策略。

模拟退火来源于物理上的降温退火问题——一个处于很高温度的物体，现在要给它降温，使物体内能降到最低。我们常规的思维是，越快越好，让它的温度迅速地降低。然而，实际上，过快地降温使得物体来不及有序地收缩，难以形成结晶。而结晶态，才是物体真正内能降到最低的形态。正确的做法，是徐徐降温，也就是退火，才能使得物体的每一个粒子都有足够的时间找到自己的最佳位置并紧密有序地排列。开始温度高的时候，粒子活跃地运动并逐渐找到一个合适的状态。在这过程中温度也会越降越低，温度低下来了，那么粒子也渐渐稳定下来，相较于以前不那么活跃了。这时候就可以慢慢形成最终稳定的结晶态了。

这一过程演化到优化问题上就成为一种模拟退火策略（实际上深度学习中的退火可能更加广泛，大概一切有助于跳脱局部最优点，寻找更佳的全局最优点的策略都能称为退火了吧）。训练一开始使用较大的学习率，在比较大的空间上搜索较优的区域，待权重相对稳定后衰减学习率缩小搜索空间，从而取得更好的训练结果并且提高了模型的鲁棒性。

大批次训练技巧

前文已经提到，盲目增大批大小其实无益于提升训练效果，但却有各种小技巧——

1.等比例增大学习率

前边提到在满足$B<<N$的前提下等比例放大（缩小）$\epsilon$和$B$效果是相当的，既然如此，我们在增大批大小的同时等比例增大学习率不仅可以避开泛化差距问题，还有助于加速收敛速度。
而对于带动量的优化器，等比例增大 $\epsilon / ( 1 - m )$ 也能取得相同的结果（其中m为动量系数）。

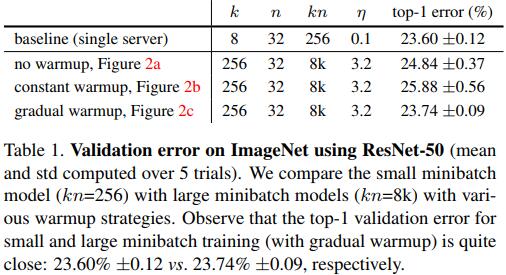
2.学习率预热

训练之初由于参数随机初始化（尤其是非预训练模型），数值上与目标参数组相去甚远，如果采用太大的学习率会出现参数数值的不稳定，不利于模型收敛。因此，从较低的学习率开始训练会比较好，比如：

  • 《Deep Residual Learning for Image Recognition(2015)》先用较低的学习率（0.01）预热，直到训练错误率低于80%之后再恢复到正常的学习率（0.1）。

    In this case, we find that the initial learning rate of 0.1 is slightly too large to start converging. So we use 0.01 to warm up the training until the training error is below 80% (about 400 iterations), and then go back to 0.1 and continue training.

  • 《Accurate, Large Minibatch SGD: Training ImageNet in 1 Hour(2017)》2.2节指出常数学习率预热会在学习率突变阶段对模型收敛产生不良印象，并提出了线性学习率预热，用斜坡来代替学习率的突变。
    lr_warmup
3.零gamma初始化

众所周知，批归一化BN通常将参数$\gamma$和$\beta$分别初始化为1和0，也就是初始状态下BN只做归一化而不做拉伸和偏移。
但对于残差单元来说，将$\gamma$初始化为1其实不一定是最佳选择，残差单元的结构如下图所示，每个卷积层之后都会接一个BN层。

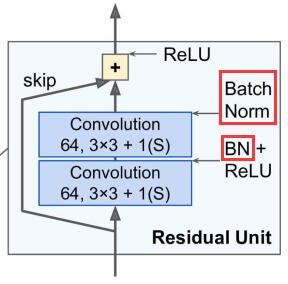
residual_unit

论文《Bag of Tricks for Image Classification with Convolutional Neural Networks(2018)》指出将第二个BN层的$\gamma$初始化为0能取得更好的结果！此时初始状态下相当于屏蔽掉了卷积层的输出，使得初始模型更加简单，有利于初始阶段模型的训练。

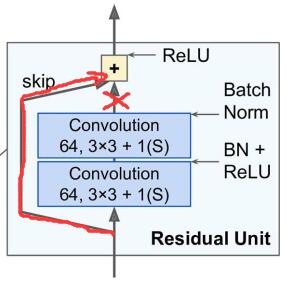
zero_gamma

该技巧同样适用于其他类似的shortcut结构。

4.无偏置衰减

作为正则化手段的一种，权重衰减经常被用来约束权重过度增长，缓解过拟合现象的发生。

除了衰减权重之外，其他参数（如偏置）能否也应用衰减技术呢？《Highly Scalable Deep Learning Training System with Mixed-Precision: Training ImageNet in Four Minutes(2018)》作者在ResNet-50和AlexNet上做了实验，结果表明，只有全连接层和卷积层的权重适合做衰减，偏置以及BN层的$\gamma$和$\beta$参数都不适合做衰减！

bn_decay_resnet50



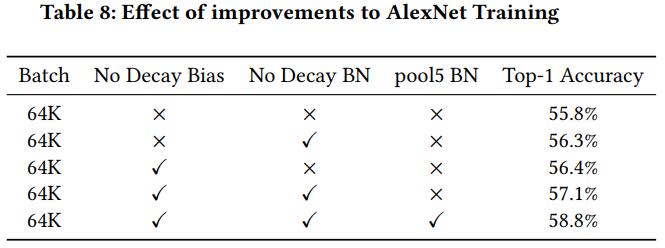
bn_bias_decay_alexnet

另外，《Large batch training of convolutional networks with layer-wise adaptive rate scaling(2018)》研究发现，在训练初期，不同层的权重的原始更新项 $\nabla L \left( w _ { t } \right)$ 和 惩罚项 $||\omega||$ 相差悬殊，比如迭代一次后的AlexNet——

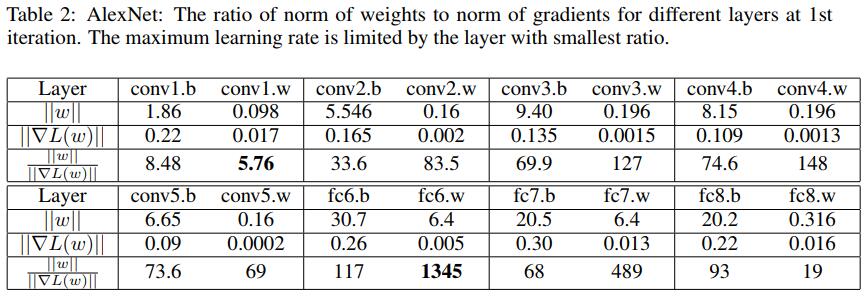
lars_alexnet_ratio

这使得训练初期模型的收敛方向对初始权重和初始学习率十分敏感，而导致模型发散、不容易收敛。于是论文提出了层级自适应比例缩放（Layer-wise Adaptive Rate Scaling, LARS），其每层的在每次更新时的学习率都是根据梯度和权重的比例计算出来的：
将原始的SGD更新项
$$\Delta w _ { t } = \lambda * \nabla L \left( w _ { t } \right)$$

改造为
$$\triangle w _ { t } ^ { l } = \gamma * \lambda ^ { l } * \nabla L ( w _ { t } ^ { l } )$$

其中，$w_t^l$第$l$层的权重，$\gamma$ 用于学习率变化的全局策略（比如整体衰减等），$\lambda^l$ 表示第$l$层的学习率，且
$$\lambda ^ { l } = \eta \times \frac { \left| w ^ { l } \right| } { \left| \nabla L \left( w ^ { l } \right) \right| }$$
其中，$\eta < 1$ 参数反映了我们对“随机梯度$\nabla L \left( w _ { t } ^ { l } \right)$与真实梯度很接近”的信任程度，越接近（比如批大小越大时，随机梯度就跟真实梯度越接近），那么$\eta$参数就可以设置越大。

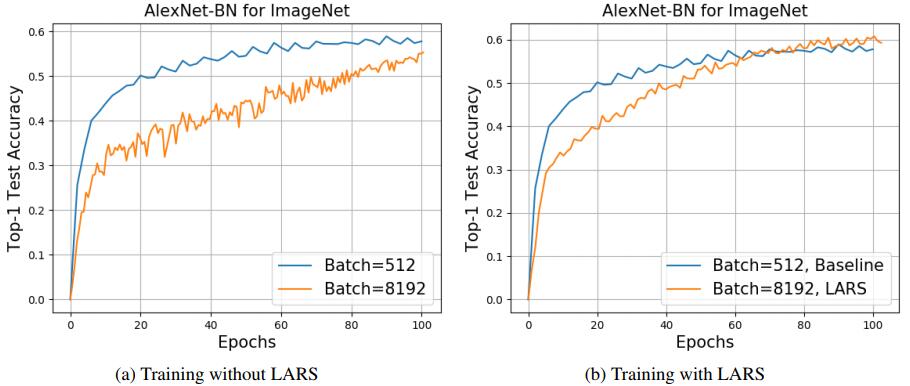
应用LARS之后，模型收敛速度变得更快——

alexnet_lars

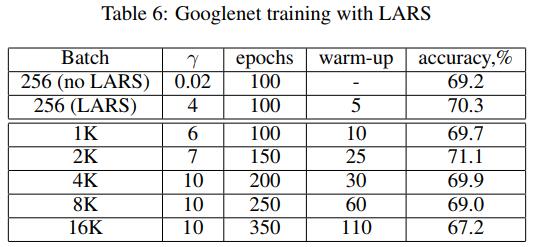
而且对于分类任务，batch_size在16K以内都不会有明显的负面影响——

googlenet_lars

低精度训练

现在新出的GPU陆续开始支持低精度FP16计算，并且计算速率远高于FP32，比如V100就提供了100TFLOPS的FP16计算，而其FP32只有14TFLOPS。
论文《Mix Precision Training(2017)》提出一种混合精度的训练过程——

  • 用FP16存储所有的参数和激活
  • 用FP16计算梯度
  • 每份参数都保留一份FP32副本用于更新（更新后再转为FP16）
  • 为损失乘以一个缩放因子使得FP32的梯度可以更好得跟FP16数据对齐（论文3.2节）
    由于FP32比FP16拥有更多的数据位保存指数部分，使得相对于FP16，FP32可以保存小得多或大得多的数值，那么当数值超出FP16范围时就会被截断而导致训练过程中梯度消失或扩散，最终模型发散无法收敛。论文经过实验表明，给FP16的梯度乘以8（即增加三位的指数部分）就足以使训练结果与纯FP32的结果相当。

论文经过实验证明，即使使用混合精度也可以训练出跟纯FP32接近的效果——

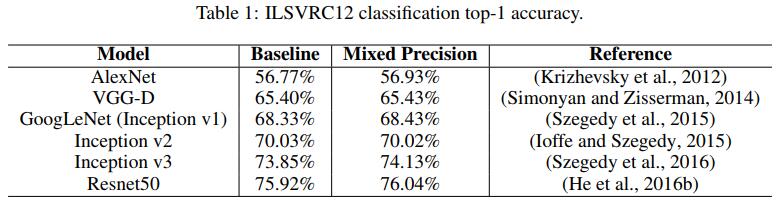
mixed_precision_result

而且在检测任务上，如果不对损失进行缩放对齐，有可能会导致训练发散——

mixed_precision_detection

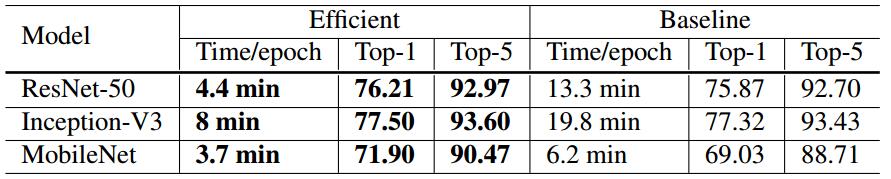
实验结果

baseline：批大小256，FP32
efficient：批大小1024，FP16

efficient_results