1 绪论、线性回归与逻辑回归
绪论
- 机器学习的过程
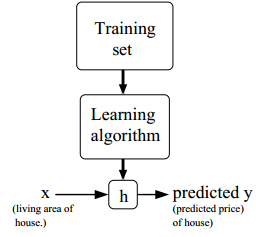
其中h为一个预测函数,称为hypothesis - 监督学习和非监督学习
监督学习的训练数据是一组带标记的数据
非监督学习的训练数据是一组无标记的数据,由学习器完成聚类任务 - 分类问题 & 回归问题
若推测的结果是连续的,那么这是一个回归问题
若推测的结果是离散的,那么这是一个分类问题
线性回归
- 基本模型:($h_\theta(x)$可以简写为$h(x)$,$\theta$为模型参数或称为权重,默认$x_0 = 1$即所表示的项为常数项)
$$h_\theta(x) = \sum_{i=0}^{n} \theta_i x_i = \theta^T x$$ - 成本函数(cost function)
$$J(\theta) = \frac{1}{2} \sum_{i=1}^{m} ( h_\theta(x^{(i)}) - y^{(i)} )^2$$
式中之所以有系数 $\mathbf{ \frac{1}{2} }$ ,是为了J在求导时系数为 1
这是常见的成本函数——最小二乘
LMS(Least Mean Squares)算法
寻找最优的参数$\theta$,使成本J最小
梯度下降(gradient descent)算法
考虑单一参数,
$$\theta_j := \theta_j - \alpha \frac{\partial}{\partial \theta_j} J(\theta)$$
代入、求偏导可得
$$\theta_j := \theta_j + \alpha( y^{(i)} - h_\theta( x^{(i)} ) ) x_j^{(i)}$$
其中,
$x_j^{(i)}$表示第i个样本的第j个特征值
$\alpha$是学习速率,$\alpha$太小,算法收敛速度太慢;$\alpha$太大,则会出现振荡现象
$( y^{(i)} - h_\theta ( x^{(i)} ) )$为误差项
再考虑多个参数,有两种更新方式——
- 批梯度(batch gradient descent)下降
$$
\begin{aligned}
&重复直到收敛\{\\
&&\theta_j := \theta_j - \alpha \sum_{i=1}^{m} ( y^{(i)} - h_\theta( x^{(i)} ) ) x_j^{(i)} (所有\theta_j同时更新)\\
&\}
\end{aligned}
$$
$h_\theta(x^{(i)})$与$\theta_j$有关,这里要求所有$\theta_j$同时更新。换句话说,每次循环中参与计算的$\theta_j$统一取上次循环中的值而不是取本次循环的更新值
每次更新都需要扫描整个数据集 - 增量(incremental)梯度下降 或 随机(stochastic)梯度下降
$$
\begin{align}
&重复直到收敛\{\\
&&\text{for i = 1 to m}\{\\
&&&\theta_j := \theta_j - \alpha ( y^{(i)} - h_\theta( x^{(i)} ) ) x_j^{(i)} (所有\theta_j同时更新)\\
&&\}\\
&\}
\end{align}
$$
每次只用一个样本进行更新,虽然难以收敛到最优解(会在最优解附近振荡),但一般来说是足够近似的
- 描述参数与成本函数的关系
- 绘制$J - \theta$图像(一般是单参数的平面图)
- 绘制轮廓图(一般是双参数的平面图)
横轴、纵轴分别代表一个参数
类似地理的等高线,绘制等J线(一个个的椭圆),往往椭圆越小,代表的J的值就越小
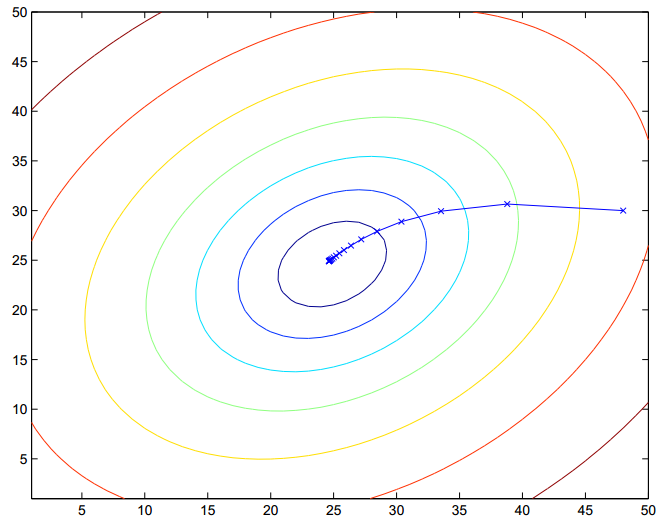
- 梯度下降算法得到的最优解是“局部最优解”
其解与初始点的选取有关,可以随机选取多个初始点分别寻找各自的“局部最优解”
然后从这些“局部最优解”中找到“最优”的一个作为“全局最优解” - 描述收敛速度
绘制 成本函数-迭代次数 图像,观察成本函数的收敛速度
梯度下降算法通常需要多次迭代,一般会为算法设置一个迭代次数 或是 一个误差目标
正规方程算法
- 迹算子tr
$$trA = \sum_{i=1}^{n} A_{ii}$$- $trAB = trBA$
- $trA = trA^T$
- $tr(A+B) = trA + trB$
- $traA = atrA$
- 矩阵导数(Matrix derivatives)
f对A的导数——
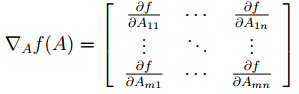
其中f是矩阵A到一个实数域的映射- $\triangledown_A trAB = B^T$
- $\triangledown_{A^T} f(A) = (\triangledown_A f(A))^T$
- $\triangledown_A trABA^TC = CAB + C^TAB^T$
- $\triangledown_A |A| = |A| (A^{-1})^T$
- 嗯!没错!经过一番奇妙的推导~
$$\triangledown_\theta J(\theta) = X^TX\theta - X^T\vec{y}$$
令$\triangledown_\theta J(\theta) = 0$,则
$$X^TX\theta = X^T\vec{y}$$
即
$$\theta = (X^TX)^{-1}X^T\vec{y}$$ $X^TX$不可逆的问题
通常数据量会比较大,很少存在不可逆的问题;
如果出现了不可逆,常见的可能原因有:- 冗余特征:存在强依赖关系的特征,如x1=2x2
特征太多,样本太少,导致矩阵行数小于列数
解决方法:正则化?对于octave有两种求逆函数
- pinv函数求未逆,即使矩阵不可逆依旧能使算法正常执行得出结果
- inv函数求真正的逆,如果矩阵不可逆则算法会出错
带权重的线性回归
- 普通的线性回归
找到合适的参数$\theta$最小化$\sum_{i=1}^{m} ( h_\theta(x^{(i)}) - y^{(i)} )^2$
误差函数是固定的,根据已知的数据集得到参数,从而确定一个回归模型,用该模型去预测新的数据 - 带权重的线性回归
找到合适的参数$\theta$最小化$\sum_{i=1}^{m} \omega^{(i)}( h_\theta(x^{(i)}) - y^{(i)} )^2$
其中$\omega^{(i)} = exp( -\frac{( x^{(i)} - x )^2}{2\tau^2} )$,即预测的结果离实际值越大则样本的权重越大,而参数$\tau$则描述了这个权重的差异;
这是一个非参数学习算法,误差函数随预测值的不同而不同,$\theta$无法事先确定,每次预测都需要临时进行计算而不能直接套用模型
逻辑回归
逻辑回归其实是讨论的是分类问题,而不是回归问题
sigmoid函数
代价函数
- 《机器学习实战》中逻辑回归采用和线性回归一样的代价函数
即$J(\theta) = \frac{1}{m} \sum_{i=1}^{m} \frac{1}{2} ( h_\theta(x) - y )^2$
记$Cost( h_\theta(x), y ) = \frac{1}{2} ( h_\theta(x) - y )^2$
在逻辑回归中容易出现很多个局部最优解,难以找到全局最优
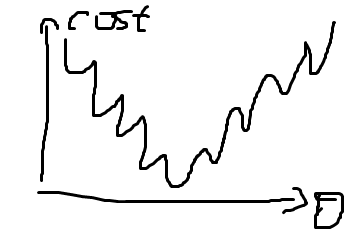
- 吴恩达这里采用新的cost函数
$$
\begin{equation}
Cost( h_\theta(x), y ) = \left\{
\begin{aligned}
& -log( h_\theta(x) ), & y = 1\\
& -log( 1 - h_\theta(x) ), & y = 0
\end{aligned}
\right.
\end{equation}
$$
可以写成
$$Cost( h_\theta(x), y ) = -ylog(h_\theta(x)) - (1-y)log(1-h_\theta(x))$$
如下图所示,分类的偏差越大,代价增长得越快——
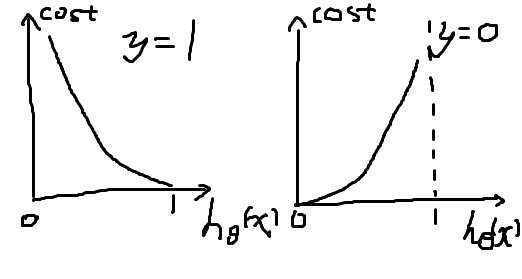
通常逻辑回归使用的代价函数——
$$J(\theta) = -\frac{1}{m} \sum_{i=1}^{m}[ y^{(i)} log h_\theta(x^{(i)}) + (1-y^{(i)}) log (1 - h_\theta(x^{(i)})) ]$$ - 梯度下降算法
$$\theta_j := \theta_j + \alpha( y^{(i)} - h_\theta( x^{(i)} ) ) x_j^{(i)}$$
其形式同线性回归的梯度下降算法,但此处的假设$h_\theta(x^{(i)})$并不同——
对于线性回归,
$$h_\theta(x{(i)}) = \theta^Tx$$
对于逻辑回归,
$$h_\theta(x{(i)}) = \frac{1}{1+e^{-\theta^Tx}}$$ - 其他高级算法
这些算法比较复杂,但无需手动选择学习速率$\alpha$,而且收敛速度更快- Conjugate gradient共轭梯度算法
- BFGS变尺度算法
- L-BFGS限制变尺度算法
多分类问题
一个n分类问题可以转化为$C_n^2$个二分类问题,
即(是A/不是A)、(是B/不是B)、……
计算出所有可能的预测概率,取最大者作为预测分类