优化器
BGM:《文豪野犬》ED1
唔,就是它,因为这个番才认识太宰治和芥川
参考《Hands-On Machine Learning with Scikit-Learn and TensorFlow(2017)》Chap11
《Hands-On Machine Learning with Scikit-Learn and TensorFlow》笔记
常见的加速训练技术
常见的优化器有:Momentum optimization, Nesterov Accelerated Gradient, AdaGrad, RMSProp, Adam optimization
其中Adam optimization是目前表现最好的优化器;不过它除了学习率之外还有额外两个超参数需要手工调整
传统梯度下降
$$ \theta \gets \theta - \eta \bigtriangledown_\theta J(\theta) $$
固定的下降速度(梯度作为速度)
动量法(Momentum optimization)
论文:Some methods of speeding up the convergence of iteration methods(1964)
$$ m \gets \beta m + \eta \bigtriangledown_\theta J(\theta), 0 <= \beta <= 1 $$
$$ \theta \gets \theta - m $$
梯度作为加速度使用,这里m表示动量;
引入新的超参数 $\beta$ 与先前的 $m$ 相乘,以继承先前的动量,并防止动量过快增长;
当$\beta=0$时为完全摩擦(退化为传统梯度下降),当$\beta=1$时为完全光滑,通常来说取$\beta=0.9$
此时下降速度变为:$ \frac{1}{1-\beta} \eta \bigtriangledown_\theta J(\theta) $
取$\beta=0.9$时,下降速度理论上变为传统梯度下降的10倍!!
具体实现:
optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.9)
涅斯捷罗夫加速梯度(Nesterov Accelerated Gradient, NAG)
又称Nesterov Momentum optimization
论文:A method of solving a convex programming problem with convergence rate O(1/k^2)(1983)
$$ m \gets \beta m + \eta \bigtriangledown_\theta J(\theta + \beta m), 0 <= \beta <= 1 $$
$$ \theta \gets \theta - m $$
动量法的变体,比动量法更快,而且振荡更小;
与动量法相比,区别在于计算的是损失函数在 $\theta + \beta m$ 上而不是 $\theta$ 上的梯度: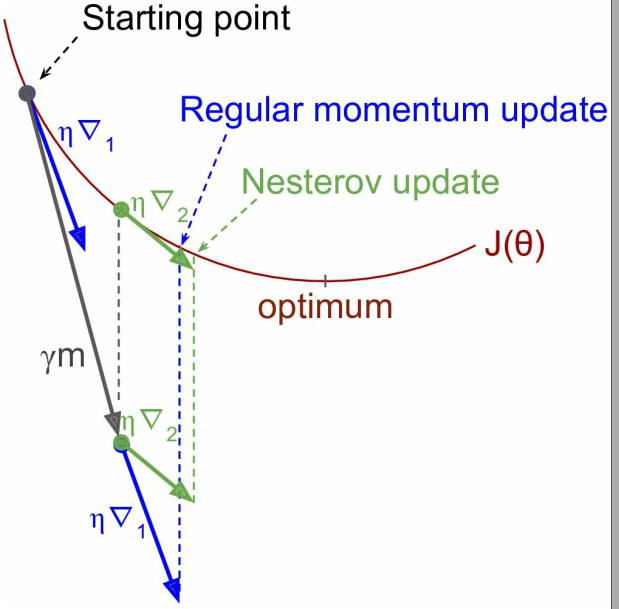
具体实现:
# 与动量法的优化器一样,只不过打开了nesterov开关
optimizer = tf.train.MomentumOptimizer(learning_rate=learning_rate, momentum=0.9, use_nesterov=True)
AdaGrad
论文:Adaptive Subgradient Methods for Online Learning and Stochastic Optimization(2011)
$$ s \gets s + \bigtriangledown_\theta J(\theta) \otimes \bigtriangledown_\theta J(\theta) $$
$$ \theta \gets \theta - \eta \bigtriangledown_\theta J(\theta) \oslash \sqrt{s+\epsilon} $$
其中,
$\otimes$ 表示逐项相乘,$\oslash$ 表示逐项相除;
$s$ 继承上一次的 $s$,并且累加一个梯度的平方(如果沉浸在某个权重方向上,那么更新速度会越来越快);
$\theta$ 的更新与传统梯度下降类似,不过更新时梯度除以一个 $\sqrt{s+\epsilon}$,$\epsilon$ 通常取 $10^{-10}$ 防止 $s=0$ 的情况;
考虑两权重梯度差异显著的情况(如图,$\theta_1$ 平缓,$\theta_2$ 陡峭),
传统的梯度下降,会在陡峭的 $\theta_2$ 上很快到达一个比较的位置,而平缓的 $\theta_1$ 方向上梯度下降缓慢;
而AdaGrad能够检测到这种特殊情况,从而加速梯度下降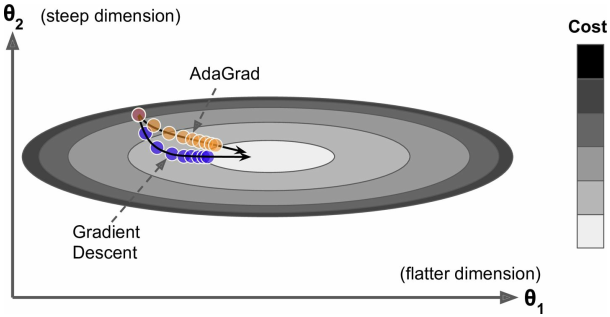
简而言之,AdaGrad衰减了学习率,但是会在沉浸的权重方向上加速更新;
其学习过程中,学习率是自适应的,这有助于更佳直接地找到全局最优点,而且更容易调整超参数 $\eta$
tensorflow中提供了相应的 AdagradOptimizer 优化器
AdaGrad在一些简单的任务如线性回归上可能会比较高效
RMSProp
该优化器由eoffrey Hinton在其课堂上提出,而没有形成正式的论文,研究者通常用 slide 29 in lecture 6 来引用它;
幻灯片:http://www.cs.toronto.edu/~tijmen/csc321/slides/lecture_slides_lec6.pdf
视频:https://www.youtube.com/watch?v=defQQqkXEfE&list=PLoRl3Ht4JOcdU872GhiYWf6jwrk_SNhz9&index=29
AdaGrad的变体,解决了AdaGrad学习率衰减偏快的问题
$$ s \gets \beta s + (1-\beta) \bigtriangledown_\theta J(\theta) \otimes \bigtriangledown_\theta J(\theta) $$
$$ \theta \gets \theta - \eta \bigtriangledown_\theta J(\theta) \oslash \sqrt{s+\epsilon} $$
通常,$\beta$ 取0.9
具体实现:
optimizer = tf.train.RMSPropOptimizer(learning_rate=learning_rate, momentum=0.9, decay=0.9, epsilon=1e-10)
Adam optimization
论文:ADAM: A METHOD FOR STOCHASTIC OPTIMIZATION(2015)
集成动量法和RMSProp的思想——
$$ m \gets \beta_1 m + (1-\beta_1) \bigtriangledown_\theta J(\theta) $$
$$ s \gets \beta_2 s + (1-\beta_2) \bigtriangledown_\theta J(\theta) \otimes \bigtriangledown_\theta J(\theta) $$
$$ m \gets \frac{m}{1-\beta_1^T} $$
$$ s \gets \frac{s}{1-\beta_2^T} $$
$$ \theta \gets \theta - \eta m \oslash \sqrt{s + \epsilon} $$
其中,T表示迭代次数(从1记起)
通常,取 $\beta_1 = 0.9, \beta_2 = 0.999, \epsilon = 10^{-8}, \eta = 0.001$
Jacobian优化 & Hessian优化
以上讨论都是基于一次偏导的Jacobian矩阵,实际上用基于二次偏导的Hessian矩阵可以取得更好的优化效果;
但这很难应用到DNN上,因为每层都会输出 $n^2$ 个Hessian矩阵(如果是Jacobian,只需要n个),其中n是参数数量,而DNN参数数量大的惊人,所以基于Hessian的优化反而会因为计算大量的Hessian矩阵而速度下降并且需要大量的空间来进行计算;
训练稀疏模型
有时候需要一个占据空间少、预测时间短的稀疏模型,可以采用以下技术进行稀疏化:
- 用常规的方式训练模型,然后将数值很小的权重置为0
- 用L1惩罚项进行正则化
- 使用Dual Averaging技术(也叫Follow The Regularized Leader, FTRL)
论文:Primal-dual subgradient methods for convex problems(2009)
tensorflow也提供了相应的优化器FTRLOptimizer,它是根据Ad Click Prediction: a View from the Trenches(2013)实现的,是FTRL的变体
学习计划(learning schedules)
如图,当学习率太低时训练过慢,学习率太高时不容易得到最优解;
可以在开始训练时给一系列不同的学习率跑一小段时间,比较它们的loss曲线,来确定一个比较合适的学习率;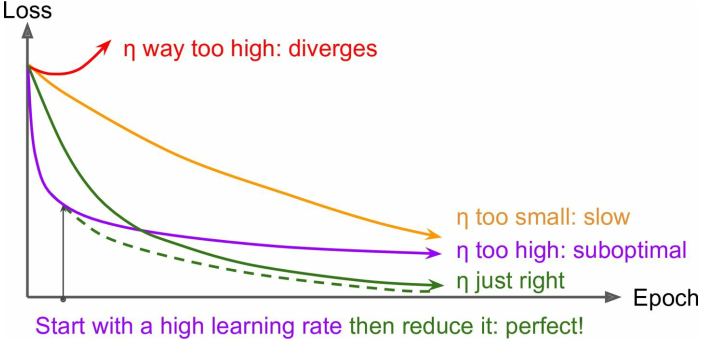
除此之外,还有一些有用的策略,称为学习计划learning schedules——
- 分段常数学习率(Predetermined piecewise constant learning rate)
预设好每过多少epochs就改变学习率;需要比较多的人工调整 - 性能调整(Performance scheduling)
每N步用验证集计算一次loss,当loss不再减小的时候衰减学习率(通常乘以一个因子 $\gamma$) - 随时间指数衰减(Exponential scheduling)
$$ \eta(t) = \eta_0 10^{-t/r}, t为迭代次数 $$
需要人工调整参数 $\eta_0$ 和r,学习率每r步衰减一次; - 随时间乘方衰减(Power scheduling)
$$ \eta(t) = \eta_0 (1+t/r)^{-c} $$
通常取 $c=1$,有点类似Exponential scheduling,但衰减速度稍微慢一些
论文AN EMPIRICAL STUDY OF LEARNING RATES IN DEEP NEURAL NETWORKS FOR SPEECH RECOGNITION(2013) 比较了一些主流的学习计划——
在语音识别任务中使用动量法优化的前提下,
- performance scheduling和exponential scheduling都表现的很好
- 但是exponential scheduling容易实现、容易调整、收敛更快
具体实现:
initial_learning_rate = 0.1
decay_steps = 10000
decay_rate = 1/10
global_step = tf.Variable(0, trainable=False)
learning_rate = tf.train.exponential_decay(initial_learning_rate, global_step, decay_steps, decay_rate)
optimizer = tf.train.MomentumOptimizer(learning_rate, momentum=0.9)
training_op = optimizer.minimize(loss, global_step=global_step)
由于AdaGrad, RMSProp和Adam optimization等优化器具有自适应调整学习率的能力,因而不需要额外的学习计划来衰减学习率;