2019中兴捧月·总决赛
赛题背景
与初赛类似,不过初赛更多关注的是加速,而总决赛更关注的是压缩。
原始模型是一个简单的3x112x112输入大小的resnet18,人脸识别项目,主办方提供了两万张无标签的校准数据集,和两千张带标签的本地验证数据集,同时主办方保留两千张私有、不公开的测试数据集。
评分规则如下:
$$ score = \left( \left( \frac { M - m } { M } \right) \times 20 + \left( \frac { S - s } { s } \right) \times 80 \right) \times A ( z ) \times B ( z )$$
$$A ( z ) = \left\{ \begin{array} { l l } { 1 , } & { z \geq 0.97 } \\ { 0.9 , } & { 0.965 \leq z < 0.97 } \\ { 0 , } & { z < 0.965 } \end{array} \right.$$
$$B ( z ) = \left\{ \begin{array} { l l } { 1 , } & { s \leq 40 M B } \\ { 0.9 , } & { 40 M B < s \leq 50 M B } \\ { 0.8 , } & { 50 M B < s \leq 63 M B } \\ { 0 , } & { s > 63 M B } \end{array} \right.$$
其中,$M$、$S$分别为原始模型的内存占用大小、模型文件大小,$m$、$s$、$z$分别是压缩后的内存占用大小、模型文件大小、万分之一误检率下的正检率。主要参照本地验证数据集(一千个人,每人两张图片)的z值,私有测试集只用于模型泛化能力的参考(防止选手故意过拟合于验证集)。
压缩方案
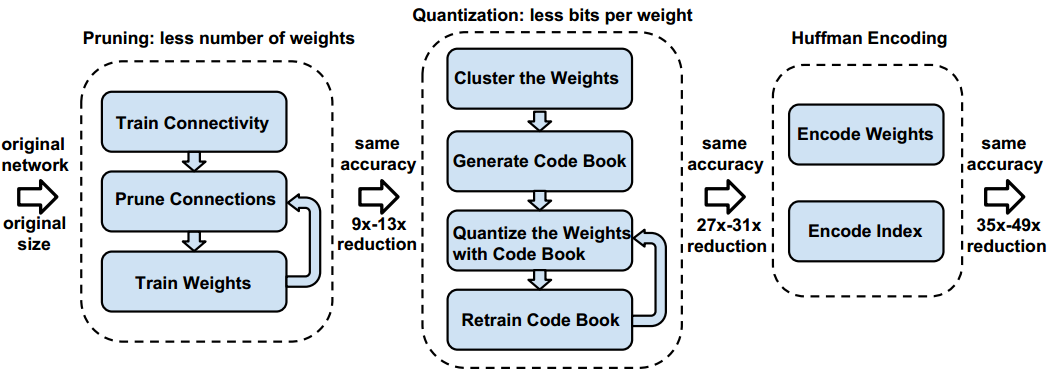
总体思路参考论文《Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding(2016)》,采用剪枝-量化-哈夫曼编码三步走的压缩策略。
剪枝
粒度
按照论文《Exploring the Regularity of Sparse Structure in Convolutional Neural Networks(2017)》,剪枝的粒度按不规则(非结构)到规则(结构)可以分为fine-grained(精细的神经元层面的剪枝,也称为netron)、vector(向量,以卷积核的某一行或列为单位)、kernel(核,以输入通道为单位)、filter(滤波器,以输出通道为单位),除此之外其实还有以layer或block为单位进行裁剪,但相对比较暴力,实用中比较少见。
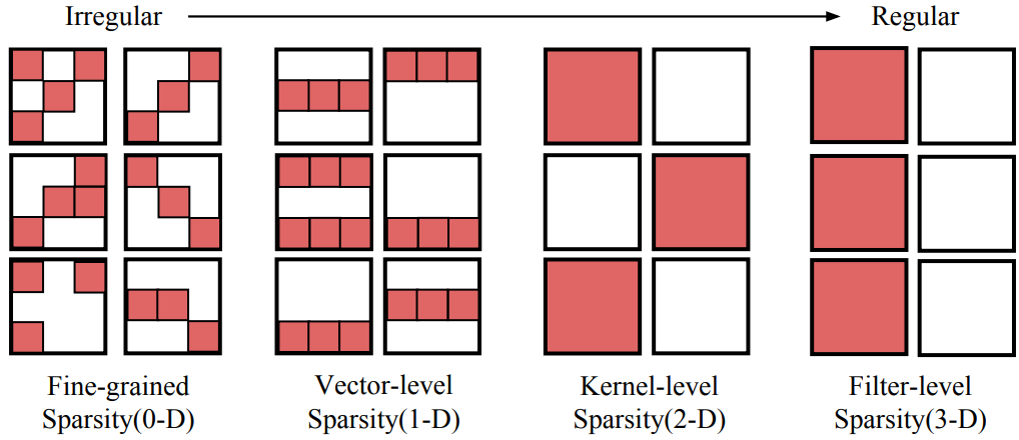
在上述粒度中,最为常见的是fine-grained(netron)和filter,前者因为采用精细化的裁剪,往往可以取得更高的压缩率,但需要搭配稀疏存储、稀疏计算技术使用;后者有比较高的结构性,往往配合以kernel为单位的裁剪(前一层裁掉filter后,后一层可以相应的裁剪kernel),不依赖于额外的存储和计算技术,而且有直接、明显的速度提升,适合加速网络。
本次赛题以压缩为主,故自然而然地采用fine-grained(netron)的剪枝方案。
剪枝标准
在fine-grained(netron)级别的剪枝中通常采用某个阈值作为剪枝标准,最简单的阈值可以通过人为设置,也可以设置一个剪枝的百分比。而论文《Learning both Weights and Connections for Efficient Neural Networks(2015)》则采用敏感度(sensitivity)作为剪枝的标准——
$$sensitivity = std ( \text {weight} ) * s$$
计算十分简单,直接统计一个层里权重的标准差,然后乘以一个人为设定的系数$s$作为剪枝的阈值。
众所周知,
- 神经网络的第一层卷积比较敏感;
- 全连接层的冗余性远高于卷积层
所以我简单的分了三档系数,以普通的卷积层的剪枝系数为$s$,分别设定第一层卷积、最后的全连接层为$0$和$2s$。
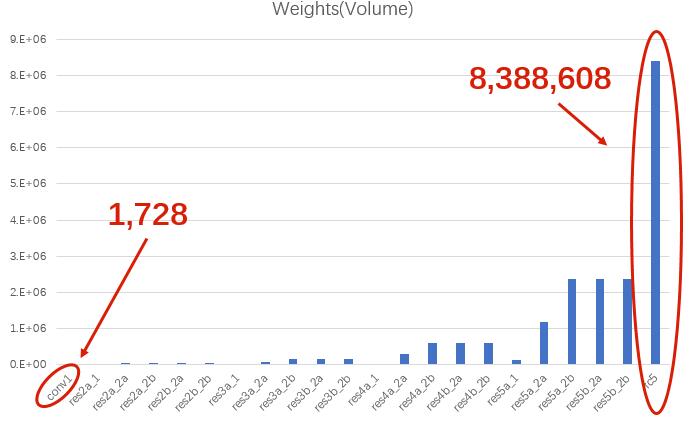
事实上,第一层卷积主要是对量化比较敏感,还是可以轻裁的,只不过我后续把稀疏存储和哈弗曼编码写在了一起,如果只裁剪不量化就需要拆解代码,加上第一层卷积只有1728个参数(相比之下全连接层可是有足足8,388,608个参数),剪枝的压缩空间非常小,所以这里索性不对第一层卷积进行裁剪。
恢复训练
如果能对剪枝后的模型进行简单的训练,模型可以有效的恢复精度。而本次比赛只给了两万张无标签的校准数据,常规的训练是行不通的,但既然有原始模型,我们不妨采用知识蒸馏的策略对剪枝后的模型进行恢复训练。
向原始模型依次投喂这两万张数据,并保存其输出作为恢复训练的标签;
loss可以采用简单的距离度量,比如L2、cosine,还可以采用KL散度(又称为相对熵)——实践表明,KL散度的效果略优于L2和cosine。决赛时也有大佬融合了L2和cosine作为loss,我自己尚未做过测试,不知道相比之下效果如何。
恢复训练通常有两种形式,
- 直接一刀剪枝,然后一次性fine-tune到最佳效果;
- 逐层剪枝,每次剪枝后都进行fine-tune到最佳效果再进行下一次剪枝;
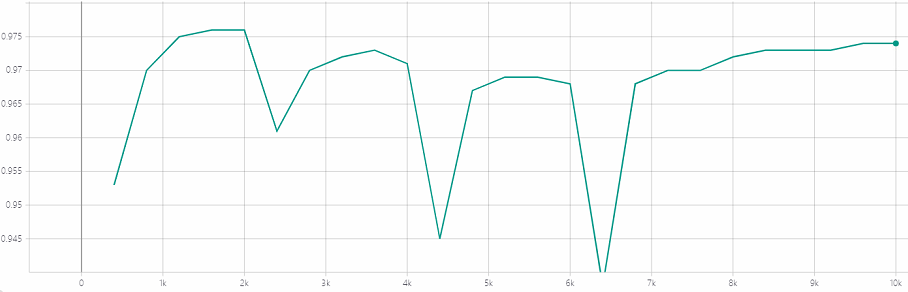
前一种方式简单粗暴,但无疑第二种方式往往可以取得比较好的结果。可第二种方式往往也是最费时的,比赛时间有限,所以我采取了论文《To prune, or not to prune: exploring the efficacy of pruning for model compression(2017)》用的折中方案——每次多剪一点点,然后简单的fine-tune(但不fine-tune到最佳效果),最后达到目标剪枝结果后再进行彻底的fine-tune。
稀疏存储
netron级别的剪枝往往需要搭配稀疏存储和稀疏运算来实现,比如对于密集的矩阵数据存储方式,每个非零数值可以改为(行序, 列序, 数值)的三元组进行存储,甚至可以展平后按(索引, 数值)的二元组进行存储,只要稀疏度足够高,这种存储方式就能获得收益。
论文《Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding(2016)》甚至对该方式进行了简单的改进,采用二元组存储,但使用相对索引而不是绝对索引——
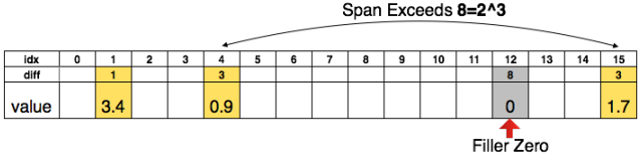
当非零元素之间的距离超过最大值时,通过补0值的方式来保证相对索引的正常工作。
量化
按量化后数值的分布进行简单地划分,量化可以分为均匀分布的量化和非均匀分布的量化,前者因为可以将浮点运算转换为整型运算而大幅提高模型推理速度,所以更为常见;后者不得不依赖查表运算,对推理速度的提升毫无帮助,但由于量化过程中聚类中心(可以把量化看成一种权重共享,聚集成$2^n$类)不再需要“均匀分布”这一约束,往往能对量化后的模型造成更小的损失,也意味着可以采用更低位数的量化方式。
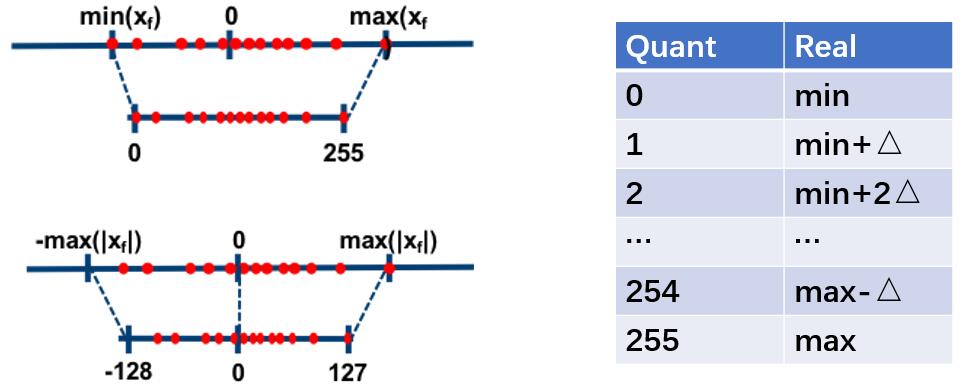
与剪枝类似,在训练过程中融入模拟量化有助于减少量化造成的模型精度损失,也即论文《Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference(2018)》提到的Quantization-Aware Training,先前在《MXNet上的重训练量化 | Hey~YaHei!》一文中有所提及,这里就不再赘述。
非均匀分布的量化的训练过程则有些不同,如论文《Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding(2016)》采用KMEANS进行聚类,训练过程中用量化后的权重前向传播,反向传播时则将所有梯度按类别分组求和,最后乘以学习率(也即SGD方式)来更新聚类中心。
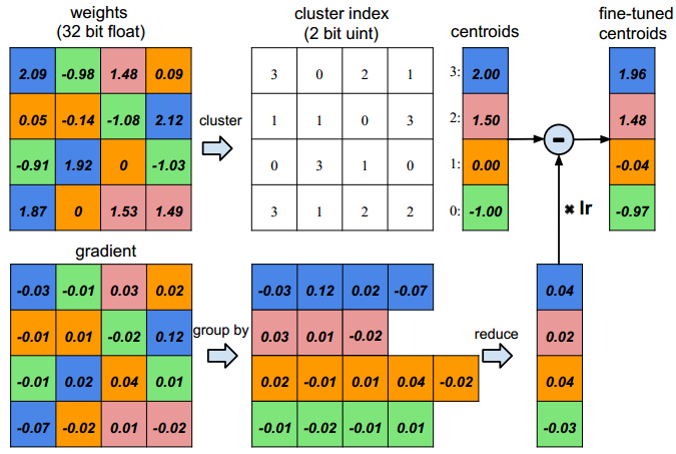
原本在参加比赛前已经写好了训练代码,在有硬标签的ImageNet上工作正常,但到了决赛现场换成知识蒸馏的方式后训练就不断出现问题,最后比赛时间有限也没来得及解决,所以量化这一块由于没用上重训练,也没有做出很好的效果。
哈夫曼编码
哈夫曼编码是根据数值出现的频次分配不等长的位数进行表示的压缩编码方式,与量化乃是天然的技术组合,也广泛应用在各类文件压缩技术当中。
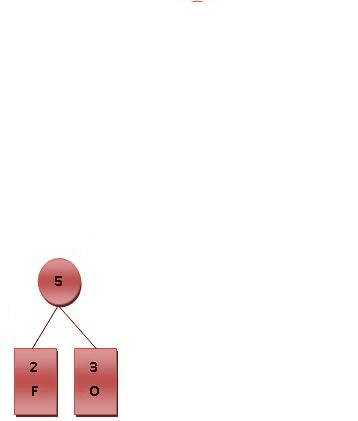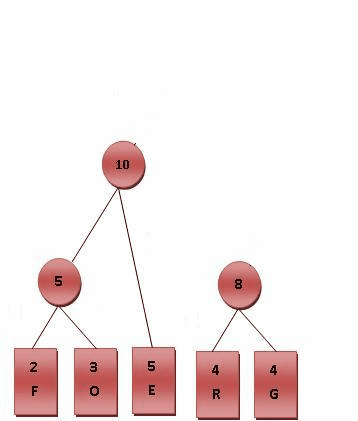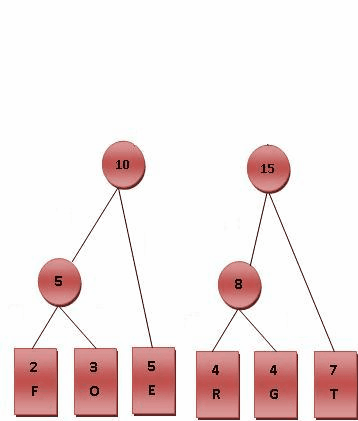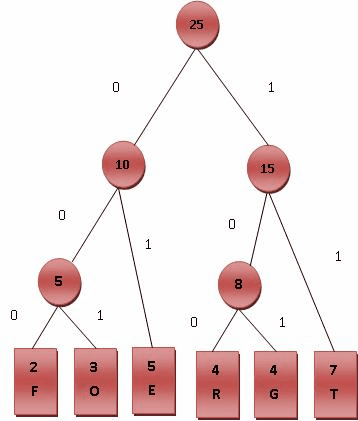
以数值0、1、2为例,假设0值的出现频率远高于1、2,那么如果构建如下图所示的哈夫曼树:
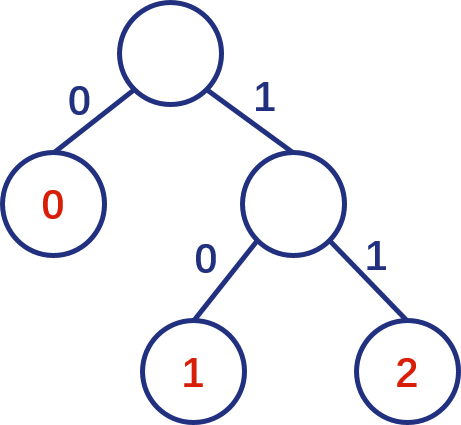
将0编码为0b0,将1编码为0b10,将2编码为0b11;此时0值只需要一个bit就能表示,当0值出现频率足够高时,则整体的数据串具有压缩的效果,如——

压缩效果
应用剪枝、量化、哈夫曼编码后,模型大小从74.5MB减少到6.9MB,验证集上精度(万分之一误检率下的正检率)仅从97.3%下降为97.2%,各层剪枝情况、量化位数、哈夫曼编码后的平均位数、整体压缩率如下表所示:
| Layer | Sparsity | Weight Bits | Weight Bits(H) | Index Bits | Index Bits(H) | Rate(P+Q) | Rate(P+Q+H) |
|---|---|---|---|---|---|---|---|
| conv1 | – | – | – | – | – | – | – |
| res2a_1 | 77.56% | 7 | 8.21 | 5 | 3.35 | 91.59% | 91.89% |
| res2a_2a | 82.18% | 7 | 6.69 | 5 | 2.65 | 93.32% | 94.79% |
| res2a_2b | 67.48% | 7 | 6.18 | 5 | 2.36 | 87.81% | 91.32% |
| res2b_2a | 55.63% | 7 | 6.23 | 5 | 2.13 | 83.36% | 88.40% |
| res2b_2b | 53.96% | 7 | 6.18 | 5 | 1.96 | 82.73% | 88.28% |
| res3a_1 | 58.36% | 7 | 6.83 | 5 | 2.40 | 84.39% | 87.99% |
| res3a_2a | 48.08% | 7 | 5.97 | 5 | 1.91 | 80.53% | 87.21% |
| res3a_2b | 52.51% | 7 | 5.80 | 5 | 2.04 | 82.19% | 88.35% |
| res3b_2a | 52.68% | 7 | 5.85 | 5 | 2.07 | 82.25% | 88.28% |
| res3b_2b | 56.35% | 7 | 5.76 | 5 | 2.04 | 83.63% | 89.37% |
| res4a_1 | 54.75% | 7 | 6.17 | 5 | 2.21 | 83.03% | 88.14% |
| res4a_2a | 47.52% | 7 | 5.53 | 5 | 1.90 | 80.32% | 87.82% |
| res4a_2b | 52.11% | 7 | 6.01 | 5 | 2.06 | 82.04% | 87.92% |
| res4b_2a | 48.99% | 7 | 5.70 | 5 | 1.96 | 80.87% | 87.80% |
| res4b_2b | 51.80% | 7 | 5.49 | 5 | 1.99 | 81.93% | 88.73% |
| res5a_1 | 53.95% | 7 | 5.92 | 5 | 2.14 | 82.73% | 88.41% |
| res5a_2a | 48.01% | 7 | 5.75 | 5 | 1.92 | 80.51% | 87.54% |
| res5a_2b | 46.93% | 7 | 5.64 | 5 | 1.88 | 80.10% | 87.51% |
| res5b_2a | 48.41% | 7 | 5.67 | 5 | 1.94 | 80.65% | 87.73% |
| res5b_2b | 49.19% | 7 | 5.57 | 5 | 1.94 | 80.95% | 88.08% |
| fc5 | 73.97% | 4 | 3.33 | 5 | 3.19 | 92.68% | 94.69% |
| total | 59.79% | 85.97% | 90.81% |
注意到res2a_1的Weigths Bits(H),其哈夫曼编码后占用的空间反而比直接的紧凑存储(七位紧凑存储,而非按字节存储)高,这是因为其编码前的数值出现频次相对均衡造成的(构建的哈夫曼树会是一棵平衡树或相对平衡的树)。
关于内存
起初一听说决赛会考量运行时的内存占用大小,立马就想起了直接卷积——天下没有免费的午餐,任何加速算法都需要额外的代价,而这个代价往往就是额外的占用空间,卷积也是如此——还有什么比最朴素的for循环卷积更省空间的吗?
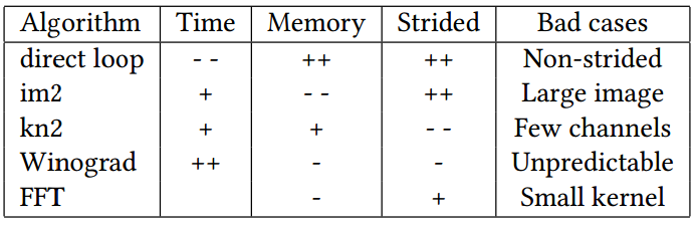
再加上KMEANS的量化方式不得不采用查表法实现推理,在比赛前我就用纯C++写好了一个神经网络……甚至越陷越深,试图取巧地用紧凑存储的方式把权重存储在内存上(本来想做稀疏存储的,但时间来不及)。
最后评委也没认可我这种查表法的处理方式(摊手.jpg),而且只看“加载权重后的内存占用”而不看“前向推理的内存占用”,所以决赛时内存部分也没拿到几分……唉~
后记
答辩PPT:点击下载
一直都是一个人瞎捣鼓着模型压缩的东西,碰巧看到有这么一个比赛所以想去试试,起初也没想过能拿奖,摸着摸着初赛竟然拿到第一,决赛虽然有些遗憾但也已经远远超出最初的预期,而且在比赛过程中学习效率极高,又认识了非常多可爱的人儿,专家组、HR、还有所有的选手都相当棒!!还认识了非常优秀的一等奖大佬(我大三那会儿可啥都不会,jh真是太强了!),——已经十分满足了哈~(๑¯∀¯๑)
这里的6.9MB也不是最优的结果——首先决赛疏忽大意,剪枝前忘记做一下SVD;此外,剪枝部分给量化预留了太多的空间,事实上还能多裁几刀;按照经验,即使是用上均匀分布的量化,通过重训练应该也能用更少的bit位数(而不是7bits和4bits)来进一步压缩——个人估计压缩到5MB以内应该也没啥问题。
应主办方要求,总决赛这部分只能公开一下文档,代码就不便开源啦。
DeepCompression的实现可以稍微参考一下Deep-Compression-PyTorch | Github, mightydeveloper,但他有些部分做的不够完美(比如稀疏存储部分没有使用论文的相对索引导致最终的模型偏大,而且也没实现量化的重训练)。