傻乎乎~傻乎乎~傻乎乎~~~~~~~

呼~终于到了解读论文《Bag of Tricks for Image Classification with Convolutional Neural Networks(2018)》的最后一部分。

---

余弦学习率衰减（Cosine Learning Rate Decay）

论文：《SGDR: Stochastic Gradient Descent with Warm Restarts(2016)》

先前《深度学习小技巧（一）：高效训练 - 学习率衰减 | Hey~YaHei!》已经讨论过学习率衰减的问题啦，它本质上是一种模拟退火策略，通过逐步降低振荡幅度来更好的逼近最优点。而早在《优化器 - 学习计划（learning schedules） | Hey~YaHei!》我们也讨论过各种各样的衰减策略，其中指数衰减在很长一段时间中都是非常受欢迎的。

不过近年来大家突发奇想——光是逼近局部最优点哪里够用，不如想办法让它时不时来一次大震动，把它甩到另外一个位置开荒去？于是热重启技术就诞生了！
关于学习率的事情近两年其实有很多有意思的进展，比如学习率测试、周期性学习率、热重启技术，以及传统Adam的各种改进（比如最近北大和浙大本科生提出的AdamRound），这部分本文先按下不细讲，之后有时间应该会专门开一篇文章讨论学习率的问题。

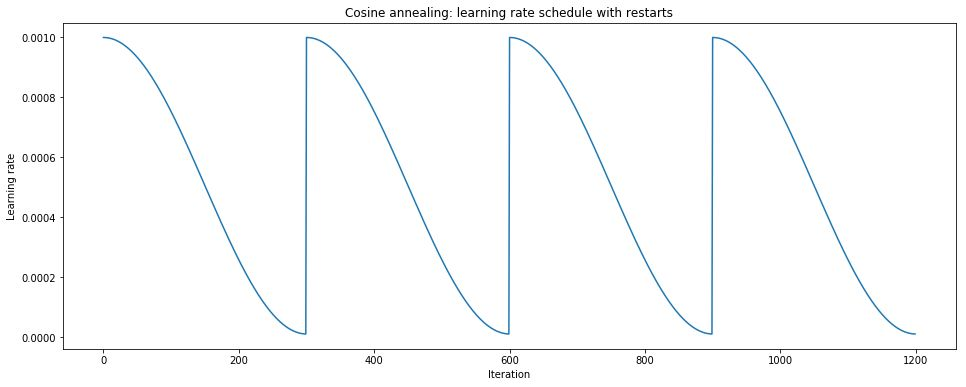
在每个周期的开始和末尾学习率变化缓慢，分别让模型有充分的时间跳出局部最优点、更逼急局部最优点；而中间部分则呈现出接近线性的下降趋势，这与周期性学习率的思想是类似的；同时每个周期开始学习率都会反弹到较高的水平，这是一种典型的模拟退火策略。

平滑标签（Label Smoothing Regularization, LSR）

该正则化技巧最初由《Rethinking the Inception Architecture for Computer Vision(2015)》提出（Chapter 7），并应用在inception-v2的训练上。

首先考虑传统的softmax和交叉熵——
$$q _ { i } = \frac { \exp \left( z _ { i } \right) } { \sum _ { j = 1 } ^ { K } \exp \left( z _ { j } \right) }$$
$$\mathrm { H } ( \mathrm { p } , \mathrm { q } ) = - \sum _ { k=1 } ^ { K } p_k \cdot \log q_k $$

通常来说，对模型最后一层全连接层的输出 $z_i$ 按第一个公式进行归一化作为各个分类的预测概率 $q_i$；训练时则应用第二个公式，对实际概率 $p_k$ 和预测概率 $q_k$ 的对数相乘求和得到损失 $H(p,q)$，训练的目标即是最小化损失 $H(p,q)$。
一般我们已知了实际分类，所以自然地用独热码的方式选取——
$$p = \delta _ { k , y } = \left\{ \begin{array} { l } { 1 , i = y } \\ { 0 , i \neq y } \end{array} \right.$$
此时实际的概率分布是一个冲激函数，论文《Rethinking the Inception Architecture for Computer Vision(2015)》指出，用冲激函数的实际概率分布进行训练是有问题的——模型会趋向去用极高的概率来输出一个分类结果（或者说，模型会倾向于“武断”），这将不利于泛化（容易发生过拟合）。

为了解决这一问题，文中提出了平滑标签LSR，将实际概率函数改造为
$$p ^ { \prime } (k) = ( 1 - \epsilon ) \delta _ { k , y } + \epsilon u ( k )$$
其中，$u(k)$ 是人为引入的一个固定分布（可以看作是为概率分布引入固定分布的噪声），并且由参数 $\epsilon$ 控制相对权重。那么对应的，交叉熵公式就可以展开为
$$H \left( p ^ { \prime } , q \right) = - \sum _ { k = 1 } ^ { K } p ^ { \prime } ( k ) \log q ( k ) = ( 1 - \epsilon ) H ( p , q ) + \epsilon H ( u , q )$$
从损失函数的角度上看，LSR相当于为损失函数增加了人为引入的先验概率 $u(k)$ 和预测概率 $q(k)$ 之间的惩罚项，并且赋予了相对权重 $\epsilon$。

inception-v2选用了均匀分布的 $u(k)$ 作为先验概率，即 $u(k) = 1 / 1000$ 并且设置相对权重 $\epsilon = 0.1$，使得top-1和top-5错误率都下降了约0.2%。

知识蒸馏（Knowledge Distillation）

论文：《Distilling the Knowledge in a Neural Network(2015)》

知识蒸馏也是模型压缩技术的一部分，以后应该会花时间细致地学习它，这里暂时不展开讲。知识蒸馏的总体思想，就是用一个训练好的大容量模型去指导一个小容量模型训练，从而得到更好的表现。

假设已经训练好一个大容量模型（比如ResNet-152），然后用它去指导另一个小容量模型（比如ResNet-50）训练，他们最后一层全连接层的输出（也就是各个分类的得分）分别为 $r$ 和 $z$，设实际标签的概率分布为 $p$，那么可以用如下损失函数进行训练，
$$H(p,z,r) = \ell ( p , \operatorname { softmax } ( z ) ) + T ^ { 2 } \ell ( \operatorname { softmax } ( r / T ) , \operatorname { softmax } ( z / T ) )$$
其中，$\ell(\cdot)$ 是基本的损失函数（如交叉熵），
$T$ 是一个超参数（Temperature），可以看作是用来设定“向老师学习的热情程度”。

数据混合（Mixup）

论文：《mixup: Beyond Empirical Risk Minimization(2017)》

经验风险最小化（Empirical Risk Minimization, ERM）

这是当前深度学习训练中最常见的思路，假设有一个学习任务，其特征为 $X$，标签为 $Y$，其实际的联合分布为 $P(X,Y)$，为任务建模 $f(x)$，其损失为 $\ell (f(x), y)$，那么可以定义期望风险
$$R ( f ) = \int \ell ( f ( x ) , y ) \mathrm { d } P ( x , y )$$
注意到分布 $P$ 在实际应用中是未知的，所以我们往往采用数据驱动的方式，投喂训练集 $\mathcal { D } = \left\{ \left( x _ { i } , y _ { i } \right) \right\} _ { i = 1 } ^ { n }$，从而估计出 $P$ 的经验分布
$$P _ { \delta } ( x , y ) = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \delta \left( x = x _ { i } , y = y _ { i } \right)$$
其中，$\delta \left( x = x _ { i } , y = y _ { i } \right)$ 是一个冲激函数（也叫狄拉克函数）
$$\delta \left( x = x _ { i } , y = y _ { i } \right) = \left\{ \begin{array} { l } { 1 , (x,y) = (x_i,y_i) } \\ { 0 , others } \end{array} \right.$$
用经验分布计算出来的风险即为经验风险
$$R _ { \delta } ( f ) = \int \ell ( f ( x ) , y ) \mathrm { d } P _ { \delta } ( x , y ) = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \ell \left( f \left( x _ { i } \right) , y _ { i } \right)$$
相应地，ERM就是通过最小化经验风险的一种训练方式。

邻域风险最小化（Vicinal Risk Minimization, VRM）

ERM用有限的数据来训练模型，直观地看，模型只要拥有足够的“记忆力”，把整个训练集的分布都原原本本地记下就可以得到一个看似“非常棒”的模型，这就是深度学习中典型的过拟合问题。
针对这一问题，论文《Vicinal risk minimization(2000)》提出了邻域风险最小化，其实思路非常简单——不再直接用训练集上的经验分布来估计实际分布，而是在经验分布的基础上引入高斯噪声，使得数据量变为“无限”（简单的数据生成），以此来缓解过拟合问题。
$$P _ { \nu } ( \tilde { x } , \tilde { y } ) = \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \nu ( \tilde { x } , \tilde { y } | x _ { i } , y _ { i } )$$
$$\nu ( \tilde { x } , \tilde { y } | x _ { i } , y _ { i } ) = \mathcal { N } \left( \tilde { x } - x _ { i } , \sigma ^ { 2 } \right) \delta \left( \tilde { y } = y _ { i } \right)$$
也即
$\tilde { x }$ 在正态分布 $\mathcal { N } \left( \tilde { x } - x _ { i } , \sigma ^ { 2 } \right)$ 上随机抽样；
$\tilde { y } = y_i$ 与ERM相同。

mixup

VRM只是给特征 $X$ 引入高斯噪声，取得了不错的成效，但好像还不够合理。mixup则提出了另一种邻域分布——
$$\tilde { x } = \lambda x _ { i } + ( 1 - \lambda ) x _ { j }$$
$$\tilde { y } = \lambda y _ { i } + ( 1 - \lambda ) y _ { j }$$
其中，$\lambda \sim Beta(\alpha, \alpha)$ 且 $\alpha \in (0, \infty)$。
简而言之，mixup将多个数据用加权的方式混合在一起，以此来估计实际分布；而当 $\alpha \rightarrow 0$时，mixup退化为ERM。

• 用三个及三个以上的数据做mixup并不会有额外的提升，反而会在训练过程中增加计算复杂度
• 在一个batch内做mixup和不同batch间做mixup带来的效果很接近，而前者对IO更友好
• 只在特征上做mixup的效果不如同时在特征和标签上都做mixup
• mixup提高了对坏样本（比如标签错误）的容忍性、对对抗样例的鲁棒性、同时也能使GAN训练过程变得稳定
• 若$\alpha \rightarrow \infty$，CIFAR-10上可以取得很低的错误率，而ImageNet上却反而会提高错误率
• 模型容量越大，训练效果对参数 $\alpha$ 就越不敏感，从而mixup能取得越好的效果

实验结果

分类任务

基本的数据增强：特定比例尺缩放、随机裁剪、水平翻转（无色域扰动）

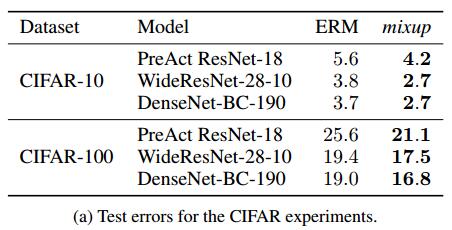
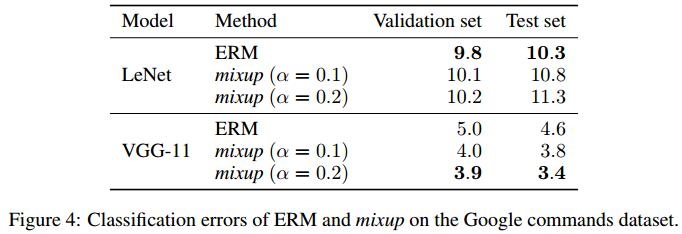
• $\alpha$ 越大，正则化效果越明显，甚至会出现欠拟合
• 容量越大的网络mixup的效果越好，而且mixup的效果往往要在训练后期才体现出来

对坏样本的容忍性测试

参考 fitting-random-labels | github, pluskid 的实验，随机将一定比例的训练数据的标签替换为随机噪声生成带坏样本的数据集进行训练。

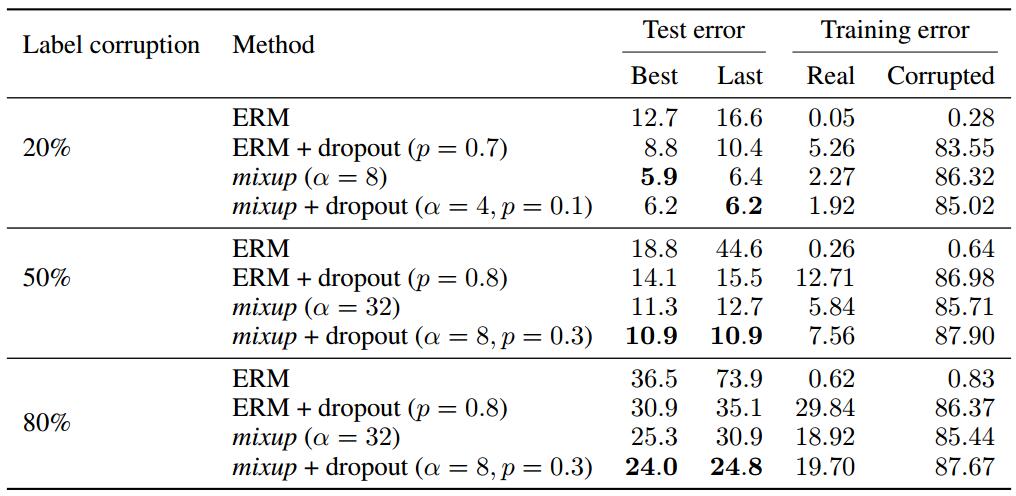
其中，Best和Last分别指最佳的测试结果、最后一个epoch的测试结果。

• mixup的效果比dropout的效果更好
• mixup和dropout是互为补充的，可以同时使用

对对抗样例的鲁棒性测试

第一次看到这种测试实验，具体还不是很理解，先放着等之后啃啃相关论文

参照论文《Intriguing properties of neural networks(2013)》生成对抗样例。

Adversarial examples are obtained by adding tiny (visually imperceptible) perturbations to legitimate examples in order to deteriorate the performance of the model. The adversarial noise is generated by ascending the gradient of the loss surface with respect to the legitimate example.

参照论文《Explaining and Harnessing Adversarial Examples(2014)》设计测试，并且得出结论：mixup有助于提高模型对对抗样例的鲁棒性。
一些指标反正现在也看不懂，就不列在这了。

切除研究（Ablation Study）

参考《In the context of deep learning, what is an ablation study? | Quora》和《什么是 ablation study？ | 知乎》。
说白了切除研究就是对照实验，控制单一变量来对比有无某一结构的结果。

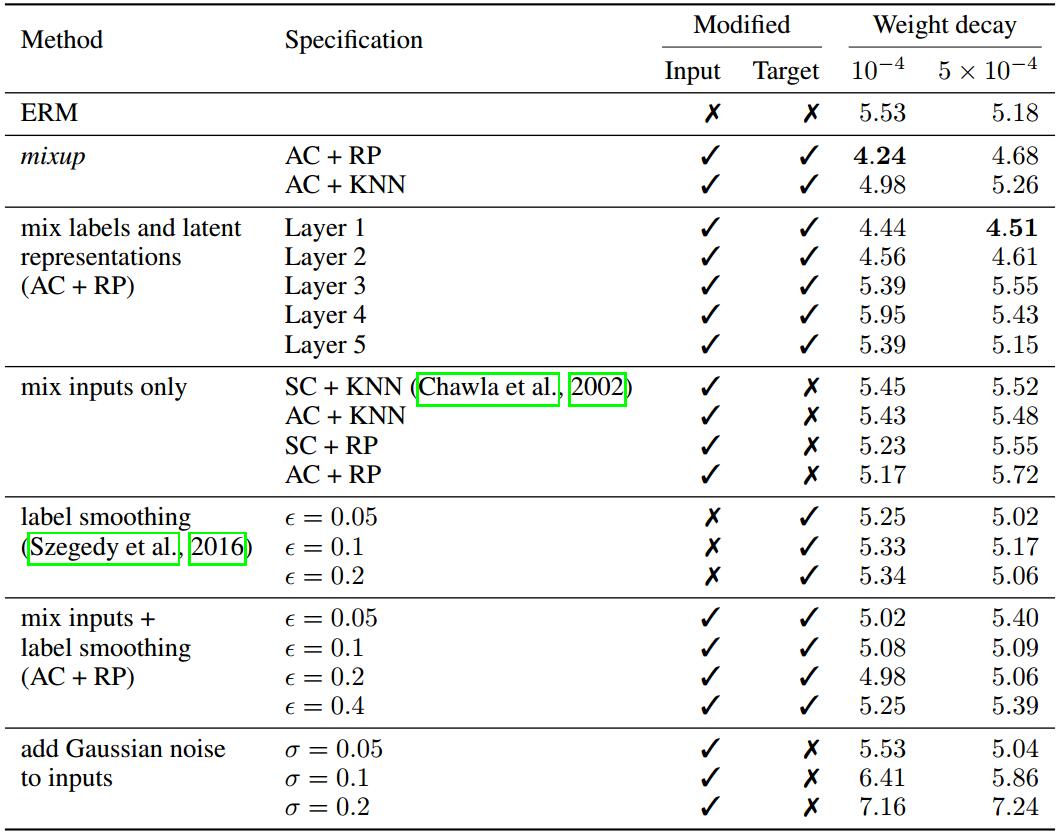
其中，
AC表示在所有分类之间做mixup，SC表示只在同一分类内做mixup；
RP表示在随机数据对之间做mixup，KNN表示在k近邻（k=200）之间做mixup。

• 随机数据对之间做mixup比k近邻效果好
• 对浅层表示做mixup似乎有点作用？但不明显，而对深层表示做mixup效果较差
• mixup的效果比标签平滑和加高斯噪声的效果好