模型参数与计算量

YaHei 1月 07, 2019

这一两个月比较忙，没什么时间空下来写写博文，加上最近处于摸索阶段，各种思路还没有理清，不敢瞎写。

这两天看到Lyken17的pytorch-OpCounter，萌生了一个写一个MXNet的计数器的想法，项目已经开源到github上，并且做个pip的包，嘻嘻……第一次做包，虽然只是一个简单的工具，还是截图留个念——
mxop-pip

参数量与计算量

参数量 是指模型含有多少参数，直接决定模型文件的大小，也影响模型推断时对内存的占用量
计算量 是指模型推断时需要多少计算次数，通常是以MAC(Multiply ACcumulate，乘积累加)次数来表示

这两者其实是评估模型时非常重要的参数，一个实际要应用的模型不应当仅仅考虑它在准确率上有多出色的表现，还应该要考虑它的鲁棒性、扩展性以及对资源的依赖程度，但事实上很多论文都不讨论他们模型需要多少计算力，一种可能是他们的定位还是纯学术研究——提出一种新的思路，即使这种思路不便于应用，但未来说不定计算力上来了，或者有什么飞跃性的改进方法来改进这一问题，或者提出自己的思路来启发其他研究者的研究（抛砖引玉）；另一种可能就是……他们在有意识地回避这一问题，我总觉得很多人是在回避这一问题，无论是论文还是各种AI比赛的解决方案（比赛本身只关注准确率指标本身也不够合理）。

接下来，我们试着用不同的视角重新审视以前那些常用的CNN OP——

全连接

首先考虑一个3输入、3输出、有偏置的全连接层（Layer2），

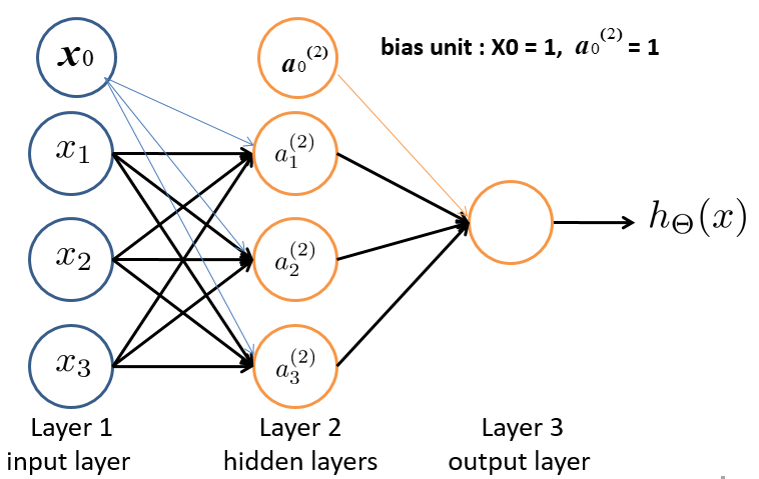
$$
\begin{array} { l } { a _ { 1 } ^ { ( 2 ) } = x _ { 0 } + w _ { 11 } x _ { 1 } + w _ { 12 } x _ { 2 } + w _ { 13 } x _ { 3 } } \\ { a _ { 2 } ^ { ( 2 ) } = x _ { 0 } + w _ { 21 } x _ { 1 } + w _ { 22 } x _ { 2 } + w _ { 23 } x _ { 3 } } \\ { a _ { 3 } ^ { ( 2 ) } = x _ { 0 } + w _ { 31 } x _ { 1 } + w _ { 32 } x _ { 2 } + w _ { 33 } x _ { 3 } } \end{array}
$$
其参数数量为 $3\times3$，乘加次数为 $3\times3$。
这是一个典型的矩阵和向量之间的乘法运算，
推广到n输入、m输出、有偏置的全连接层，其参数数量为 $m \times n$，乘加次数为 $m \times n$。

卷积

首先考虑一个单通道输入输出，输出图大小为 $m_o \times n_o$，核大小为 $k_m \times k_n$，带偏置，步长1，不补零的卷积，

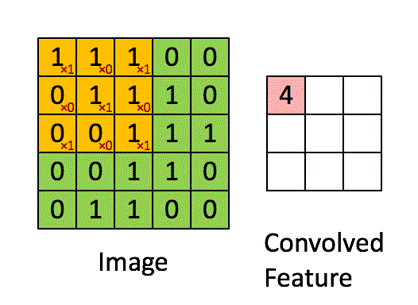
$$
\begin{aligned} O _ { 11 } = & w _ { 11 } I _ { 11 } + w _ { 12 } I _ { 12 } + w _ { 13 } I _ { 13 } + \\ & w _ { 21 } I _ { 21 } + w _ { 22 } I _ { 22 } + w _ { 23 } I _ { 23 } + \\ & w _ { 31 } I _ { 31 } + w _ { 32 } I _ { 32 } + w _ { 33 } I _ { 33 } + b \end{aligned}
$$
其参数数量为 $k_m \times k_n + 1$，乘加次数为 $m_o \times n_o \times k_m \times k_n$。
推广到$c_i$通道输入，$c_o$通道输出的情况，其参数数量为 $(k_m \times k_n + 1) \times c_i \times c_o$，乘加次数为 $m_o \times n_o \times k_m \times k_n \times c_i \times c_o$。

这是标准卷积的情况，如果是深度向分解的卷积，参考博文《MobileNets v1模型解析/深度向卷积分解/效率比较 | Hey~YaHei!》可以知道，其参数数量为 $(k_m \times k_n + c_o) \times c_i$，乘加次数为 $m_o \times n_o \times (k_m \times k_n + c_o) \times c_i$，这里为简化运算忽略了偏置。

池化

池化跟卷积的操作比较相近，最大池化仅仅是比较操作，其计算量往往可以忽略不计；平均池化则会涉及到 $m_o \times m_i \times (k_m \times k_n - 1) \times c$ 次加法和 $m_o \times n_o \times c$ 次除法（输入输出通道均为 $c$），两者都没有参数。

批归一化BN

假设输入数量为N，
$$bn[j] = \frac{\gamma (conv[j] - mean)}{\sqrt{variance}} + \beta$$
可以很容易看到，其参数数量为 $2N$，运算包含 $2N$ 次加法（包括减法）和 $N$ 次乘法。
这里要注意，在推断过程中，variance和mean都是已知的，所以 $\frac{\gamma}{\sqrt{variance}}$ 可以直接合并为一个值，
甚至，博文《MobileNet-SSD网络解析/BN层合并 | Hey~YaHei!》提到过BN层可以直接融入前边的线性层（如卷积和全连接），此时BN层不会造成任何开销。

OpSummary

hey-yahei/OpSummary.MXNet | github
知道了如何计算各层的参数数量和运算次数，我们就可以编写一个小工具来为MXNet模型统计参数数量和计算量。

钩子

为了计算运算量，必须能够取得每一层的参数、输入和输出大小，当然可以根据各层的参数一层层的推算，但这似乎太麻烦了。受Lyken17的pytorch-OpCounter启发，我们可以为每个Block注册一个hook，每次Block经过前向传播后都会调用这个hook（准确的说，有两种hook，pre_hook在前向传播前调用，hook在前向传播后调用）。

超参数获取

MXNet中想读取一个Block的超参数实在有些麻烦，因为它把超参数全都存在私有属性里了！——mxnet/gluon/nn/conv_layers.py#L105 | github，不像Pytorch的Module是直接把超参数放在公共属性上——torch/nn/modules/conv.py#L20 | github。
有两种思路来获取超参数——

从输入输出、公共变量（如Conv的weight和bias）的shape来推断
解析字符串
MXNet的Block都重载了 __repr__ 方法，比如mxnet/gluon/nn/conv_layers.py#L143 | github，用于打印Block的超参数。那……我们其实可以用 str(nn.Block) 的方式来取得这个字符串，然后进行解析= =好麻烦啊

统计

yken17的pytorch-OpCounter在统计各个模块的参数数量和运算次数时，是注册了一个公共的缓冲区来进行累加（参考pytorch-OpCounter/thop/utils | github），而MXNet并没有提供这样的缓冲区（或许只是我不知道？），我的解决办法是——
写一个拥有静态变量的函数作为累加函数，调用Block的apply方法，让每个Children把自己的统计结果依次累加给这个静态变量，最后从静态变量取出统计结果。

结果

用OpSummary把MXNet提供的model_zoo里所有的模型都测试了一遍，结果如下表所示：
Top1 Acc和Top5 Acc数据来源于 MXNet文档

Model	Params(M)	Muls(G)	*Params(M)	*Muls(G)	Top1 Acc	Top5 Acc
AlexNet	61.10	0.71	2.47	0.66	0.5492	0.7803
VGG11	132.86	7.61	9.22	7.49	0.6662	0.8734
VGG13	133.04	11.30	9.40	11.18	0.6774	0.8811
VGG16	138.63	15.47	14.71	15.35	0.7323	0.9132
VGG19	143.67	19.63	20.02	19.51	0.7411	0.9135
VGG11_bn	132.87	7.62	9.23	7.49	0.6859	0.8872
VGG13_bn	133.06	11.32	9.42	11.20	0.6884	0.8882
VGG16_bn	138.37	15.48	14.73	15.36	0.7310	0.9176
VGG19_bn	143.69	19.65	20.05	19.52	0.7433	0.9185
Inception_v3	23.87	5.72	21.82	5.72	0.7755	0.9364
ResNet18_v1	11.70	1.82	11.19	1.82	0.7093	0.8992
ResNet34_v1	21.81	3.67	21.3	3.67	0.7437	0.9187
ResNet50_v1	25.63	3.87	23.58	3.87	0.7647	0.9313
ResNet101_v1	44.70	7.59	42.65	7.58	0.7834	0.9401
ResNet152_v1	60.40	11.30	58.36	11.30	0.7900	0.9438
ResNet18_v2	11.70	1.82	11.18	1.82	0.7100	0.8992
ResNet34_v2	21.81	3.67	21.30	3.67	0.7440	0.9208
ResNet50_v2	25.60	4.10	23.55	4.10	0.7711	0.9343
ResNet101_v2	44.64	7.82	42.59	7.81	0.7853	0.9417
ResNet152_v2	60.33	11.54	58.28	11.53	0.7921	0.9431
DenseNet121	8.06	2.85	7.04	2.85	0.7497	0.9225
DenseNet161	28.90	7.76	26.69	7.76	0.7770	0.9380
DenseNet169	14.31	3.38	12.64	3.38	0.7617	0.9317
DenseNet201	20.24	4.32	18.32	4.31	0.7732	0.9362
MobileNet_v1_1.00	4.25	0.57	3.23	0.57	0.7105	0.9006
MobileNet_v1_0.75	2.60	0.33	1.83	0.33	0.6738	0.8782
MobileNet_v1_0.50	1.34	0.15	0.83	0.15	0.6307	0.8475
MobileNet_v1_0.25	0.48	0.04	0.22	0.04	0.5185	0.7608
MobileNet_v2_1.00	3.54	0.32	2.26	0.32	0.7192	0.9056
MobileNet_v2_0.75	2.65	0.19	1.37	0.19	0.6961	0.8895
MobileNet_v2_0.50	1.98	0.10	0.70	0.09	0.6449	0.8547
MobileNet_v2_0.25	1.53	0.03	0.25	0.03	0.5074	0.7456
SqueezeNet1_0	1.25	0.82	0.74	0.73	0.5611	0.7909
SqueezeNet1_1	1.24	0.35	0.72	0.26	0.5496	0.7817

由于分类网络经常用作其他框架（如目标检测的SSD）的backbone，所以这里增加了*Params列和*Muls列用于表示除去最后几个分类的Layer之后的结果。具体丢弃的层参见 mxop/tests/test_gluon_utils.py | github 文件的 dropped_layers 变量。

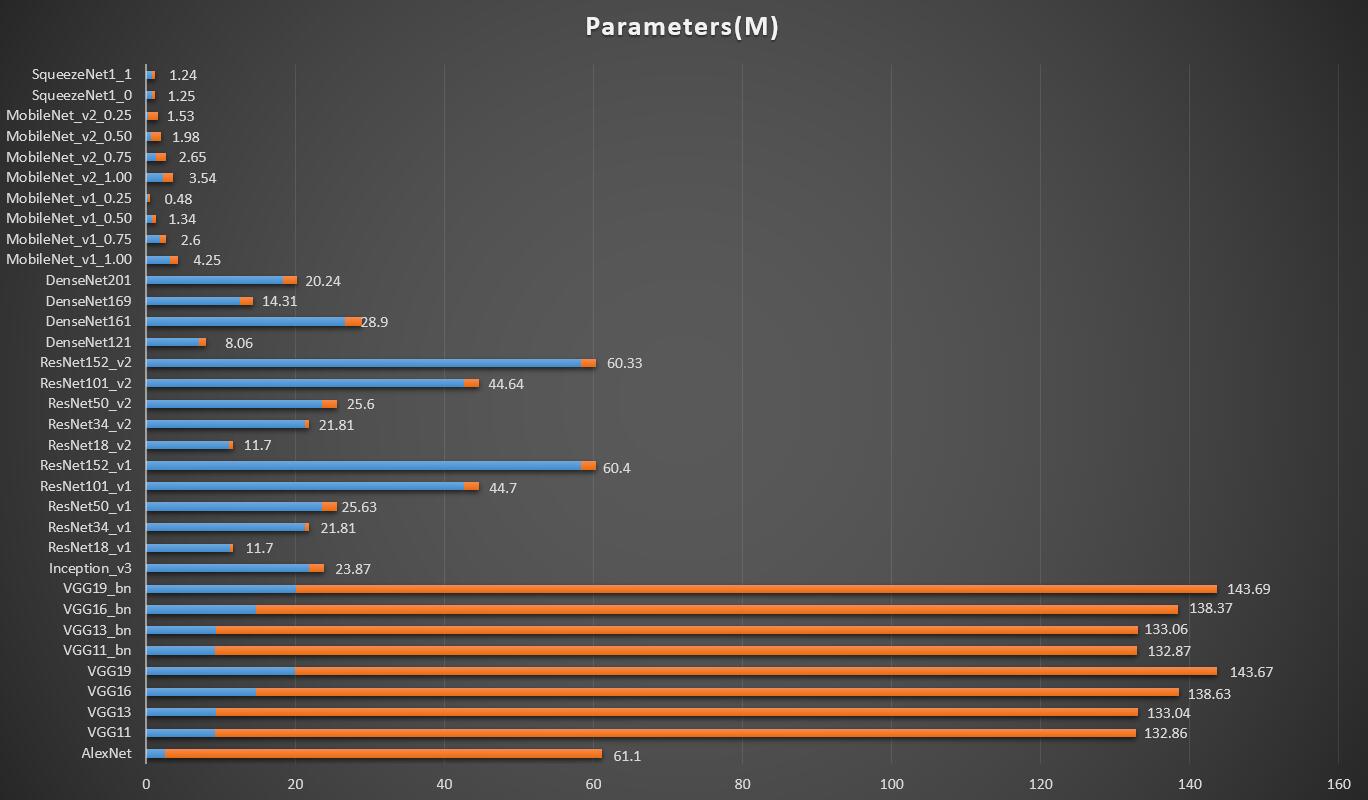
Parameters

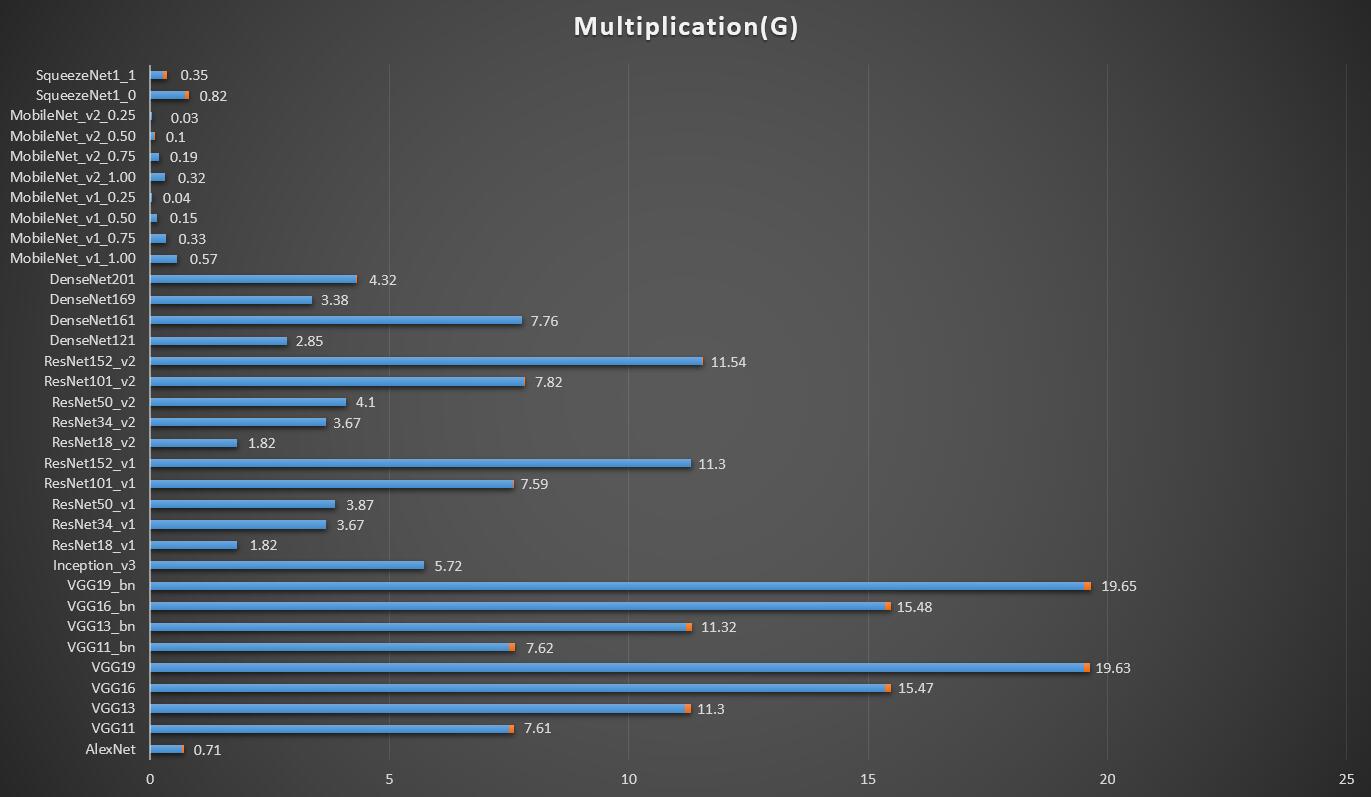
Multiplication

emmm还是比较直观的嘛！希望上述的图表对大家挑选backbone的时候能有所帮助~

下一步

目前我只模仿Lyken17的pytorch-OpCounter实现了简单的参数与计算量计数，并且制作了pip包（你可以按照我github页面上的说明用pip安装 mxop 包）；
等之后有时间，我想继续

依次输出各个层的参数与计算量而不是整个模型，分析各个层的比例
支持MXNet的静态图模型（根据json文件解析参数并推算参数量和计算量，而不是用动态图的hook）
支持MXNet的量化模型
……