SSD框架解析
上一篇文章《MobileNets v1模型解析 | Hey~YaHei!》介绍了MobileNets v1的核心思想和网络结构,本文将解析MobileNet SSD网络的另外一部分——SSD框架。SSD的主要贡献,一方面在于从多个不同尺度的特征图获取特征信息进而预测目标的位置和类别,使网络同时对输入图片上的大小物体都比较敏感;另一方面在于其训练技巧值得借鉴,这在论文中有一定的阐述,更加详细的训练技巧可以结合作者开源的代码学习。
论文:《SSD: Single Shot MultiBox Detector(2016)》
网络结构
与分析MobileNets v1模型不同,分析框架我们先从整体入手。

- 用预训练好的分类网络作为特征提取器(论文里使用的是VGG16)
VGG16原模型如下图所示:
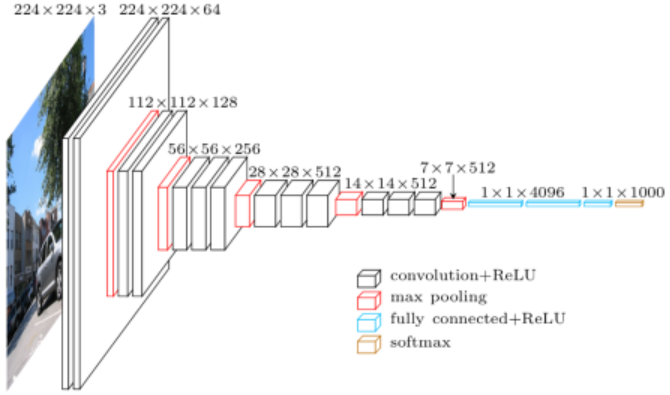
由于SSD论文里输入是 $300 \times 300$,我们重写一下VGG16模型的各层输出大小:
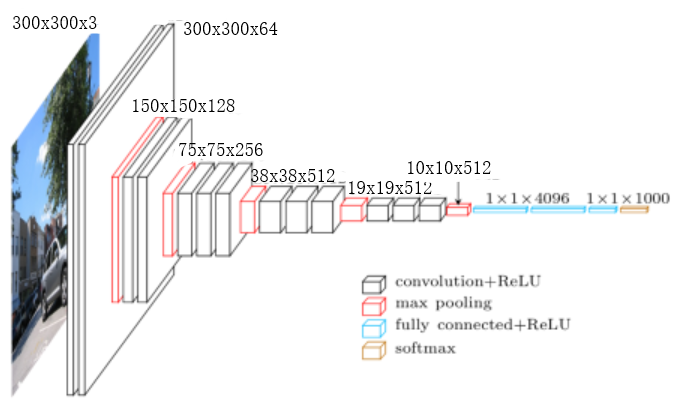
- 论文中,SSD丢掉了VGG16最后的全局池化和全连接层(FC6和FC7)
并且分别用 $3 \times 3 \times 1024$ 的卷积层Conv6和 $1 \times 1 \times 1024$ 的卷积层Conv7替代FC6和FC7作基础分类网络的最终特征抽取。 - 随后是一系列不同尺度的卷积层在不同尺度上做特征提取
- 融合不同尺度特征信息
分别用卷积操作从 $38 \times 38$ 的Conv4_3、$19 \times 19$ 的Conv7、$10 \times 10$ 的Conv8_2、$5 \times 5$ 的Conv9_2、$3 \times 3$ 的Conv10_2、$1 \times 1$ 的Conv11_2抽取特征(直接回归出后述的预测框的位置以及各分类的置信度),各自Flatten之后拼接成“长条”状特征向量。 - 非极大值抑制(Non-Maximum Suppression,NMS)
- 从置信度最高的框开始,如果其他预测框和该框的jaccard重叠率超过阈值,则丢弃
- 从剩下的框找到置信度最高的框,如果其他预测框和该框的jaccard重叠率超过阈值,则丢弃
- ……重复直到遍历所有的框
感受野和缺省框
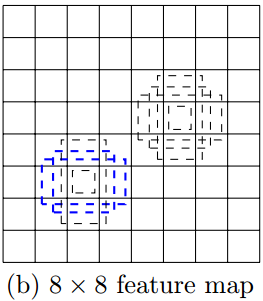
感受野
卷积是对特定小区域的特征提取,比如一张 $300 \times 300$ 的原图经过一定卷积操作之后得到 $8 \times 8$ 的特征图,特征图上的每个“像素点”其实对应原图的一个“感受野”,在这里一个“感受野”的大小为 $\frac{300}{8} \times \frac{300}{8}$ 也即 $37.5 \times 37.5$ (实际上不可能有$.5$,是$37$还是$38$要看卷积过程是否padding)。
换句话说,特征图左上角的一个感受野其实是原图左上角一个 $37.5 \times 37.5$ 大小区域的一个特征抽取(或者说是这个区域的一个抽象化,融合了这个区域的信息)。
缺省框
论文里称为default box,而源码里称为prior box.
在SSD中,为每个向Detection贡献特征的特征图上的每个感受野分配若干不同大小和长宽比(aspect ratio)的绑定框(Bounding Box),比如在作者开源的源码中,这些绑定框是这样生成的——
参考SSD - PriorBoxLayer源码 | github
(其中,$D_{min}、x_{offset}、y_{offset}、AR、D_{max}$ 都是用户指定的超参数,而且 $D_{max}$ 是可选的)
- 首先有一个最小的绑定框,其尺寸为 $D_{min} \times D_{min}$,绑定框中心相对感受野中心偏移 $(x_{offset}, y_{offset})$;
- 根据用户指定的长宽比列表 $AR$ 生成若干绑定框
对于某一特定长宽比 $AR_i$,生成尺寸分别为 $\frac{D_{min}}{\sqrt{AR_i}} \times D_{min}\sqrt{AR_i}$ 和 $D_{min}\sqrt{AR_i} \times \frac{D_{min}}{\sqrt{AR_i}}$ 的绑定框,其框中心同1; - 最后还生成一个尺寸为 $D_{max} \times D_{max}$ 的绑定框,其框中心同1;
事实上网络输出的预测框位置参数就是这每一个缺省框的中心点偏移量和长、宽偏移量(每个框共计4个参数)!
对于一个方框其实有两种不同的表示方法,都是四元组,即(中心点x坐标,中心点y坐标,长度,宽度)或(左上角x坐标,左下角x坐标,右下角x坐标,右下角y坐标)
$D_{min}$ 和 $D_{max}$ 的设置建议
论文中也给出了超参数 $D_{min}$ 和 $D_{max}$ 的设置建议——
- 首先确定框的最大最小归一化尺寸 $scale_{min}$ 、 $scale_{max}$
$$ scale = \frac{BoxSize}{ImageSize} $$
比如按论文的设计 $300 \times 300$ 的输入图片,设 $scale_{min} = 0.2、scale_{max} = 0.9$,那框的最大尺寸就是 $270 \times 270$,最小尺寸为 $60 \times 60$; - 然后最浅层的特征图对应的bbox设 $\text{min_size} = scale_{min} \times ImageSize$;
- 随后按等差数量设置各特征对应的bbox的 min_size,而 max_size 可以取下一层的 min_size(论文中默认不设置max_size);
写成数学公式为:
$$s_k = s_{min} + \frac{s_{max} - s_{min}}{m-1} (k-1), k \in [1,m]$$
其中,
$s_k$,是第k个特征图的 $min_size$ 参数;
$s_{min}$,是设计好的最小归一化尺寸,即前述 $scale_{min}$;
$s_{max}$,是设计好的最大归一化尺寸,即前述 $scale_{max}$;
$m$,是特征图的总数;
注意:上述“特征图”指的是对Detection有贡献的特征图,序号从浅层到深层递增
回过头再看看网络结构,注意从不同尺度融合特征信息的那一部分,用的都是一个 $3 \times 3$ 的卷积核,输出通道要么是 num_class + 4 的四倍要么是六倍,这里 num_class 就是最终分类的数量,数值 $4$ 其实指的是预测框的位置参数的数量,而四倍或六倍指的是特征图上每个感受野对应的绑定框数量。
按照论文,浅层的分辨率比较高,所以使用了 $AR=\{1,2,3\}$ 的分辨率组合,对于 $AR_i = 2$ 和 $AR_i = 3$ 分别会生成两个绑定框,而 $AR_i = 1$ 除了本身之外还会额外产生一个归一化尺寸为 $s’_k = \sqrt{s_k s_{k+1}}$ 的绑定框;而浅层分辨率较低,2或3的长宽比其实没太大区别或必要,所以只取了 $AR=\{1,2\}$。
源码prototxt参数示例:
layer {
name: "conv11_mbox_priorbox"
type: "PriorBox"
bottom: "conv11" # bottom[0]:特征向量
bottom: "data" # bottom[1]:原始输入(主要提供宽、高参数)
top: "conv11_mbox_priorbox"
prior_box_param {
min_size: 30.0 # 最小的基本Box大小(可根据论文计算)
aspect_ratio: 2.0 # 所要用的长宽比(除了1.0)
flip: true # 是否以0.5的概率翻转
clip: false # 是否截断Box(若截断表示不允许Box超出图片范围)
variance: 0.1 # xmin的偏差因子
variance: 0.1 # ymin的偏差因子
variance: 0.2 # xmax的偏差因子
variance: 0.2 # ymax的偏差因子
offset: 0.5 # Box中心相对于感受野中心的x、y偏移量
}
}
训练技巧
框配对(Matching)
前边讲到了感受野和缺省框,我们现在看看这些缺省框是如何跟实际标注的真实框(Ground Truth, GT)配对起来的。
介绍一个重叠率计算公式,jaccard重叠率:
$$ J(A, B) = \frac{|A \cap B|}{|A \cup B|} = \frac{|A \cap B|}{|A| + |B| - |A \cap B|} $$
对于每个GT,
- 首先,在所有缺省框中挑选出jaccard重叠率最高的一个作为配对正样本,确保每个GT都有唯一一个配对的缺省框;
- 然后,用其他缺省框挨个与GT计算jaccard,超过阈值(论文中设定为0.5)的都作为配对正样本;
- 其他未配对的都作为负样本,但显然数量上负样本远多于正样本,这会导致网络过于重视负样本而loss不稳定;
所以论文采取了Hard Negative Mining的策略,训练时按照分类的置信度为各个负样本框排序;
挑选置信度高的一批作为实际训练的负样本,同时控制负样本的数量大概为正样本的三倍左右
损失函数(MultiBoxLoss)
损失函数由位置损失 $L_{loc}$ 和分类损失 $L_{conf}$ 加权求和获得;
完整公式如下:
$$L(x,c,l,g) = \frac{1}{N} (L_{conf}(x,c) + \alpha L_{loc}(x,l,g))$$
其中,
$N$,是匹配正样本的总量(如果N=0,则令L=0);
$x$、$c$,分别是分类的指示量和置信度;
$l$、$g$,分别是预测框和GT框;
$\alpha$,是位置损失的权重。
位置损失是预测框l和真实框g之间的Smooth L1损失,
$$ L_{loc} = \sum^N_{i \in Pos} \sum_{m \in {cx, cy, w, h} x^k_{ij}} smooth_{L1} (l^m_i - \hat{g}_j^m) $$
$$ \hat{g}^{cx}_j = \frac{g^{cx}_j - d^{cx}_i}{d_i^w},\hat{g}^{cy}_j = \frac{g^{cy}_j - d^{cy}_i}{d_i^h},\hat{g}^w_j = log(\frac{g_j^w}{d_i^w}),\hat{g}^h_j = log(\frac{g_j^h}{d_i^h}) $$
其中,
$x^k_{ij}$,是指示量,当第i个匹配框和分类p的第j个真实框配对时值为1,否则为0;
$cx$、$cy$、$w$、$h$,分别是框的中心点x坐标、中心点y坐标,宽度、高度;
$d$,是绑定框(网络本身预设的绑定框);
$l$,是预测框(网络输出的加上预测偏移量的框);
$g$,是GT框(数据集标注的真实框)。
分类损失是分类置信度之间的softmax损失,
$$ L_{conf}(x,c) = -\sum^N_{i \in Pos} x^p_{ij} log(\hat{c}^p_i) - \sum_{i \in Neg}log(\hat{c}^0_i) $$
$$ \hat{c}^p_i = \frac{exp(c^p_i)}{\sum_p exp(c_i^p)} $$
源码prototxt参数示例:
layer {
name: "mbox_loss"
type: "MultiBoxLoss"
bottom: "mbox_loc" # 用于预测位置的特征向量
bottom: "mbox_conf" # 用于预测分类的特征向量
bottom: "mbox_priorbox" # 若干PriorBox的输出连接
bottom: "label" # 训练用的标签
top: "mbox_loss"
include {
phase: TRAIN
}
propagate_down: true # bottom[0] : mbox_loc,需要训练(反向传播)
propagate_down: true # bottom[1] : mbox_conf,需要训练
propagate_down: false # bottom[2] : mbox_priorbox,不需要训练
propagate_down: false # bottom[3] : label,不需要训练
# 损失计算参数组
loss_param {
normalization: VALID # 损失的归一化方式
# FULL:除以batch_size
# VALID:除以有效的数量(排除ignore_label参数指定的标签)
# NONE
}
# multibox损失参数组
multibox_loss_param {
loc_loss_type: SMOOTH_L1 # 位置预测的损失函数
conf_loss_type: SOFTMAX # 分类预测的损失函数
loc_weight: 1.0 # loc_loss的权重,论文中的alpha
num_classes: 12 # 输出类别
share_location: true # 是否让所有的预测框共享参数
match_type: PER_PREDICTION #
overlap_threshold: 0.5 # 重叠阈值(训练时超过该阈值的Box作为正样本)
use_prior_for_matching: true # 是否使用先验框(即前边是否有PriorBox)
background_label_id: 0 # 背景(background)标签的id值(与labelmap.prototxt文件匹配)
use_difficult_gt: true # 是否使用difficult的Ground Truth(?)
neg_pos_ratio: 3.0 # 负样本:正样本 的比例
neg_overlap: 0.5 # 负样本阈值(低于该阈值的Box作为负样本)
code_type: CENTER_SIZE # bounding box的编码方式
ignore_cross_boundary_bbox: false #
mining_type: MAX_NEGATIVE # 挖掘类型
# NONE:什么都不用,会发生正负样本步均衡
# MAX_NEGATIVE:为负样本排序,选择分类得分最高的一批作为训练的负样本
# HARD_EXAMPLE:选择基于“在线硬示例挖掘的基于训练区域的对象探测器”的硬实例(?)
}
}
数据增强(Data Augmentation)
目标检测任务和图片分类任务不同,
- 图片分类任务可以随意对分类对象(也即整张图片)作伸缩变换
- 目标检测任务只能对整张图片作伸缩变换,却不能对分类对象直接作伸缩变换
基本的数据增强,每张图片在输入会等概率地选取以下一种变换:
- 原始图片
- 随机裁剪
- 带jaccard重叠率约束的随机裁剪(论文给出的是0.1, 0.3, 0.5, 0.7, 0.9五种重叠率设置)
随机裁剪是有条件的,限制最低归一化尺寸(论文中为0.1),以及长宽比(论文中为$[1/2,2]$);
实际操作中是先生成一系列满足条件的框,在从中挑选若干框来裁剪图像输入训练。
仔细思考一下会发现,上述的数据增强方式只能对某个目标进行放大(zoom in)操作,这会导致小目标数据集缺失。
于是论文中在执行上述数据增强前又增加了一步缩小(zoom out)的增强措施——
- 首先生成一张画布,画布的长宽是原图片的1-4倍(随机数);
- 将原图放在画布的随机位置上;
- ……接下来再送给前述的基本数据增强步骤
据论文介绍,该额外操作为mAP提升了两到三个百分点。
对于画布,从源码data_transform.cpp/ExpandImage()函数(第489行) | github上看,是用空格符初始化了一个字符串缓冲区来作为画布,这似乎意味着是用RGB(32,32,32)的固定颜色填充了画布(空格符的assic码为32);
这种做法有些残暴,或许用原图的平均值、或者一个随机值来作固定颜色填充效果会更好一些;
甚至,用实际图片作为背景图可能会取得更好的效果,具体结论还有待实验。
源码prototxt参数示例:
layer {
name: "data"
type: "AnnotatedData"
top: "data"
top: "label"
include {
phase: TRAIN
}
# 图像转换参数组
transform_param {
scale: 0.007843 # 归一化,1/127.5
mirror: true # 0.5的概率镜像翻转
mean_value: 127.5 # 去均值(R通道)
mean_value: 127.5 # 去均值(G通道)
mean_value: 127.5 # 去均值(B通道)
# 缩放参数组
resize_param {
prob: 1.0 # 缩放操作的概率
resize_mode: WARP # 缩放模式
# WARP:放大或缩小以适应(width, height)
# FIT_SMALL_SIZE:
# FIT_LARGE_SIZE_AND_PAD:
height: 300 # 缩放后的高
width: 300 # 缩放后的宽
# 插值模式同opencv
interp_mode: LINEAR # 线性
interp_mode: AREA # 像素区域重采样
interp_mode: NEAREST # 最近邻
interp_mode: CUBIC # 三次样条
interp_mode: LANCZOS4 # Lanczos
}
emit_constraint {
emit_type: CENTER
}
# 色彩扭曲参数组
distort_param {
brightness_prob: 0.5
brightness_delta: 32.0
contrast_prob: 0.5
contrast_lower: 0.5
contrast_upper: 1.5
hue_prob: 0.5
hue_delta: 18.0
saturation_prob: 0.5
saturation_lower: 0.5
saturation_upper: 1.5
random_order_prob: 0.0
}
# 图像扩展参数组(zoom-out)
expand_param {
prob: 0.5 # 概率
max_expand_ratio: 4.0 # 扩大倍数(4x4)
}
}
# 数据源参数组
data_param {
source: "trainval_lmdb/" # 源文件
batch_size: 24
backend: LMDB # 数据源类型
}
# AnnotatedData参数组
annotated_data_param {
# 采样器1:原图
batch_sampler {
max_sample: 1
max_trials: 1
}
# 采样器2:随机抠图(overlap=0.1)
batch_sampler {
sampler {
min_scale: 0.15 # 最小尺寸(原图的0.15倍)
max_scale: 1.0 # 最大尺寸
min_aspect_ratio: 0.5 # 最小长宽比
max_aspect_ratio: 2.0 # 最大长宽比
}
sample_constraint {
min_jaccard_overlap: 0.1 # 最小JACCARD_OVERLAP(重叠率)
}
max_sample: 1 # 最大采样数量
max_trials: 50 # 最大尝试数量(产生50个随机框,然后再筛选出1个输出)
}
# [略]采样器3:随机抠图(overlap=0.3)
# [略]采样器4:随机抠图(overlap=0.5)
# [略]采样器5:随机抠图(overlap=0.7)
# [略]采样器6:随机抠图(overlap=0.9)
# [略]采样器7:随机抠图(overlap=1.0)
label_map_file: "labelmap.prototxt" # 标签映射文件
}
}
本文介绍分析了SSD框架的核心思路和训练技巧,加上上一篇文章对MobileNet模型的解析,基本的前置理论准备完毕。在下一篇博文中,将分析chuanqi305是如何把MobileNets和SSD结合起来的——《MobileNet-SSD网络解析 | Hey~YaHei!》。