BGM：《刻刻》ED
小哥哥唱歌听起来像是有点绕舌？

参考：《卷积神经网络——深度学习实践手册(2017.05)》Chap9

目标函数（target function）、损失函数（loss function）、代价函数（cost function）是一个东西~

分类任务

记某分类任务共 $N$ 个训练样本，
网络最后的分类层第i个样本的输入特征为 $x_i$，
真实标记为 $y_i \in {1,2,…,C}$ （C为类别总数），
网络最终输出预测结果（指示每种分类的可能性） $h = (h_1, h_2, …, h_C)^T$

交叉熵（cross entropy）

又称Sotfmax损失函数，目前分类任务最常用的损失函数；
用指数变换的形式，将网络输出转换成概率——
$$ L_{cross-entropy-loss} = L_{softmax-loss} = -\frac{1}{N} \sum_{i=1}^N log( \frac{e^{h_{y_i}}}{\sum_{j=1}^C e^{h_j}} ) $$

合页（hinge）

主要在SVM中广泛使用，有时也用于神经网络模型；
设计理念为“对错误越大的样本施加越严重的惩罚”；
一般在分类任务中，交叉熵效果要略优于合页
$$ L_{hinge-loss} = \frac{1}{N} \sum_{i=1}^N max(0, 1-h_{y_i}) $$

坡道（ramp）

论文：Trading convexity for scalability(2006)
合页损失函数对噪声的抵抗能力较差，非凸损失函数的引入可以很好的解决这个问题；
而坡道损失函数、Tukey’s biweight损失函数分别是分类任务、回归任务中非凸损失函数的代表，又称“鲁棒损失函数”；
它们在误差较大的区域进行截断，使得较大的误差不会大程度地影响整个误差函数；
但其非凸性质在传统机器学习中难以优化，但得益于神经网络模型的训练机制，这点非凸性质不成问题：
$$ L_{ramp-loss} = L_{hinge-loss} - \frac{1}{N} \sum_{i=1}^N max(0, s-h_{y_i}) $$
展开为：
$$ L_{ramp-loss} = \frac{1}{N} \sum_{i=1}^N ( max(0, 1-h_{y_i}) - max(0, s-h_{y_i}) ) $$
其中，s指定了截断点的位置，如下图所示（s=-0.5）——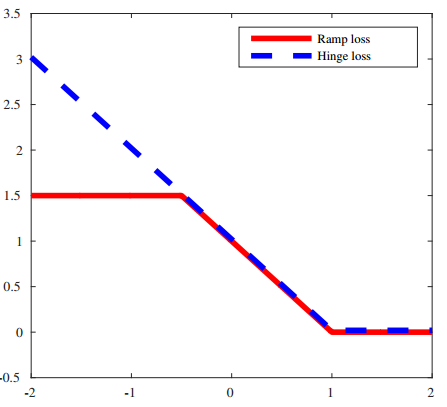

此外，论文 Robust Truncated Hinge Loss Support Vector Machines(2007) 经过理论推导指出，一般设置 $s = - \frac{1}{C-1}$

交叉熵的变体

基于交叉熵设计的新型损失函数，考虑了增加类间距离、减少类内差异等不同要素，提升网络学习特征的判别能力；

大间隔交叉熵（large-margin softmax）：
论文：Large-Margin Softmax Loss for Convolutional Neural Networks(2017)

首先考虑传统的交叉熵损失函数，根据 $h=W^T x_i$ 将其展开为——
$$ L_{softmax-loss} = -\frac{1}{N} \sum_{i=1}^N log( \frac{ e^{ W^T_{y_i} x_i } }{ \sum_{j=1}^C e^{ W^T_j x_i } } ) $$
根据内积定义进一步展开为——
$$ L_{softmax-loss} = -\frac{1}{N} \sum_{i=1}^N log( \frac{ e^{ ||W_{y_i}|| ||x_i|| cos(\theta_{y_i}) } }{ \sum_{j=1}^C e^{ ||W_j|| ||x_i|| cos(\theta_j) } } ) $$
比如二分类，传统交叉熵使得学到的参数满足 $W_1^T x_i > W_2^T x_i$，也即
$$ ||W_1|| ||x_i|| cos(\theta_1) > ||W_2|| ||x_i|| cos(\theta_2) $$
大间隔交叉熵则在上式的基础上，引入超参数m拉开两个分类的差距，即——
$$ ||W_1|| ||x_i|| cos(m \theta_1) > ||W_2|| ||x_i|| cos(\theta_2), 0<= \theta_1 <= \frac{\pi}{m} 且 m \in N^+ $$
m起到控制间隔大小的作用，m越大，类间间隔（即差距）越大，类间分类的置信度越大；当 $m=1$ 时将退化为传统交叉熵

完整定义：
$$ L_{large-margin-softmax-loss} = -\frac{1}{N} log( \frac{ e^{ ||W_{y_i}|| ||x_i|| \phi(\theta_{y_i}) } }{ e^{ ||W_{y_i}|| ||x_i|| \phi(\theta_{y_i}) + \sum_{j \ne y_i} e^{ ||W_j|| ||x_i|| cos(\theta_j) } } } ) $$
其中，
$$
\begin{equation}
\phi(\theta) = \left\{
\begin{aligned}
& cos(m \theta), & 0 <= \theta <= \frac{\pi}{m}\\
& D(\theta), & \frac{\pi}{m} < \theta < \pi
\end{aligned}
\right.
\end{equation}
$$
式中 $D(\theta)$ 只需满足“单调递减”，且 $D(\frac{\pi}{m}) = cos(\frac{\pi}{m})$ 即可；
为了简化网络前向和反向计算，论文推荐了一种具体的形式如下——
$$ \phi(\theta) = (-1)^k cos(m \theta) - 2k, \theta \in [\frac{k \pi}{m}, \frac{(k+1)\pi}{m}] $$
其中，k为整数且满足 $k \in [0, m-1]$

二分类情况下的比较——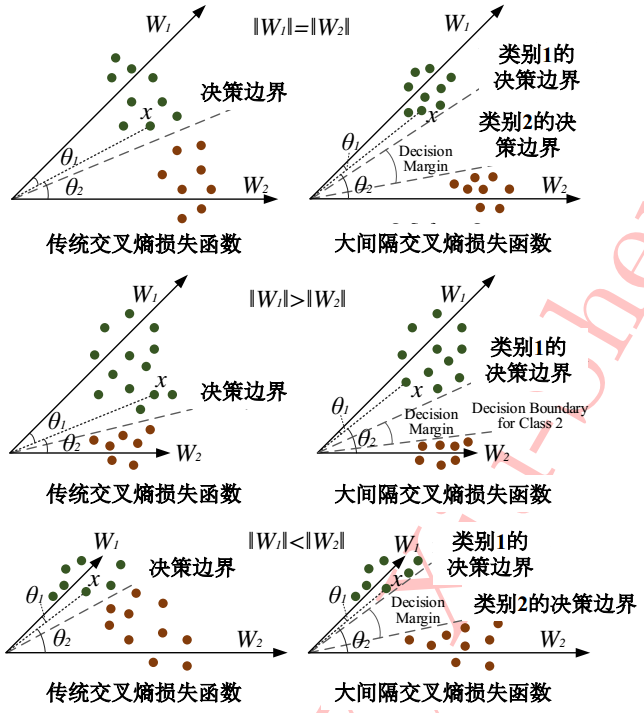

此时训练目标要比传统交叉熵损失函数更加困难；
不过好处是可以起到防止模型过拟合的作用；
在分类性能方面，大间隔交叉熵要优于传统交叉熵和合页；

中心损失函数（center loss function）：
论文：A Discriminative Feature Learning Approach for Deep Face Recognition(2016)

中心损失函数定义：
$$ L_{center-loss} = \frac{1}{2} \sum_{i=1}^N ||x_i c_{y_i} ||^2_2 $$
其中， $c_{y_i}$ 为第 $y_i$ 类所有深度特征的均值（中心）；
这将迫使样本与中心不要距离太远，否则加大惩罚；

中心损失函数只考虑了类内差异，所以通常要与考虑类间举例的损失函数（如交叉熵）配合使用，变化为——
$$ L_{final} = L_{cross-entropy-loss} + \lambda L_{center-loss}(h, y_i) $$
展开为——
$$ L_{final} = -\frac{1}{N} \sum_{i=1}^N log ( \frac{e^{h_{y_i}}}{\sum_{j=1}^C e^{h_j}} ) + \frac{\lambda}{2} \sum_{i=1}^N ||x_i - c_{y_i} ||^2_2 $$
式中，$\lambda$ 为两个损失函数之间的权衡因子，$\lambda$越大类内差异占整个目标函数的比重越大；

中心损失函数搭配传统交叉熵函数在分类性能上优于单独的传统交叉熵；
尤其在人脸识别任务上有较大的提升

回归任务

回归任务通常用残差衡量预测值和真实值的靠近程度；
记回归问题第i个输入特征 $x_i$，
真实标记为 $y^i = (y_1, y_2, …, y_M)^T$，M为标记向量的总维度；
预测值为 $\hat{y}^i$，
$l^i_t = y^i_t - \hat{y}^i_t$ 表示样本i上预测值与真实值在第t维上的预测误差；

l1、l2、Tukey’s biweight损失函数如下图所示——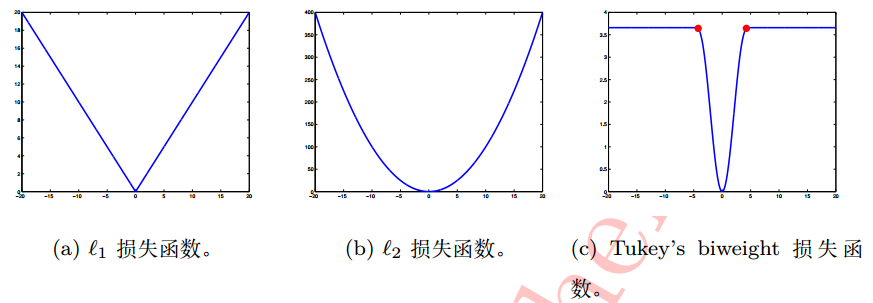

l1损失函数

$$ L_{l_1-loss} = \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^M |l^i_T| $$

l2损失函数

$$ L_{l_2-loss} = \frac{1}{N} \sum_{i=1}^N \sum_{t=1}^M (l^i_T)^2 $$
一般l1和l2在回归精度上所差无几，但一些情况下l2会略优于l1；
l2收敛略快于l1；

Tukey’s biweight损失函数

论文：Robust Optimization for Deep Regression(2015)

非凸损失函数；
定义：
$$
\begin{equation}
L_{Tukey’s-biweights-loss} = \left\{
\begin{aligned}
& \frac{c^2}{6N} \sum_{i=1}^N \sum_{t=1}^M [1-(1-(\frac{l^i_t}{c})^2)^3] , & |l^i_t| <= c\\
& \frac{c^2 M}{6}, & |l^i_t| > c
\end{aligned}
\right.
\end{equation}
$$
其中，常数c指定了函数拐点，通常取 $c=4.6851$，此时该损失函数可以与l2在最小化符合标准正态分布的残差类似的回归效果

其他任务：KL散度

实际问题往往不能简单划为回归任务或者分类任务。
如年龄估计中，经常会表达“看起来30岁左右”；
此时通常采用一个“标记的分布”来描述，如均值为30的一个正态分布；
此外，在头部倾斜角度估计、多标记分类、图像语义分割等问题上也存在类似的问题；

通常先将h转化为一个合法的分布（比如用softmax函数）；
用KL散度（Kullback-Leibler divergence）来衡量真实标记和预测分布的误差，此时也称为KL损失：
$$ L_{KL-loss} = \sum_k y_k log \frac{y_k}{\hat{y}_k} $$
因为$y_k$是已知的常量（真实标记），上式等价为：
$$ L_{KL-loss} = - \sum_k y_k log \hat{y}_k $$