Ch03 线性模型
线性回归
线性模型:$f(x_i) = \omega^T x_i + b$
将数据集(m组数据,d个属性)表示为: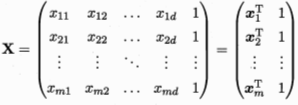
令$\hat{\omega} = (\omega ; b)$,$y = (y_1; y_2; y_3; …; y_m)$
寻找最优解(均方误差最小化):$\hat{\omega^*} = arg min_{ \hat{\omega} } (y - X \hat{\omega})^T (y - X \hat{\omega})$
广义线性模型:
考虑单调可微函数$g(\cdot)$,则$y = g^{-1}(\omega^T x + b)$是一个广义线性模型
$g(\cdot)$是一个联系函数
对数几率回归
考虑二分类任务,可以采用单位阶跃函数来进行分类
但单位阶跃函数不连续,因此不能直接作为$g^{-1}(\cdot)$
通常采用对数几率函数(对率函数,一种Sigmoid函数)来代替——
$$y = \frac{1}{1 + e^{-z}}$$
代入广义线性模型
$$y = \frac{1}{1 + e^{-(\omega^T x + b)}}$$
也即
$$ln \frac{y}{1-y} = \omega^T x + b$$
其中$\frac{y}{1-y}$是正例的相对与反例的可能性(y为正例可能性,(1-y)是反例的可能性),称为“几率”
而$ln \frac{y}{1-y}$则可以称为“对数几率”
对数几率回归的优点:
- 直接对分类可能性建模,无需事先假设数据分布
- 不仅预测出类别,还可以得到近似概率预测
- 对率函数是任意阶可导的凸函数,有很好的数学性质