吴恩达《机器学习》笔记

改进方向

• 增加训练样本
• 扩大或精简特征数量
• 增加多项式特征
• 改变正则化参数

算法评估

参考：
《机器学习》（周志华） - Ch02模型估计与选择
《机器学习》（吴恩达） - 过拟合与正则化技术

过拟合

可以画出 $h_\theta(x$ 曲线来判断是否过拟合，但一般特征有很多难以画图；
更常用的是用交叉验证的方式；

• 可以将数据随机分为训练集（一般取70%）和验证集（一般取30%）
  • 用不同的参数训练集训练学习器
  • 验证集进行交叉验证检验学习效果从而选择合适的参数，并检验算法的泛化能力
• 更好的方式是将数据随机分为训练集（一般取60%）、验证集（一般取20%）、测试集（一般取20%）
  • 用不同的参数训练集训练学习器
  • 验证集进行交叉验证检验学习效果从而选择合适的参数
  • 测试集用于检验算法的泛化能力

偏差（bias）问题 & 方差（variance）问题

训练、验证（测试）成本函数的误差error与多项式最高次d的关系——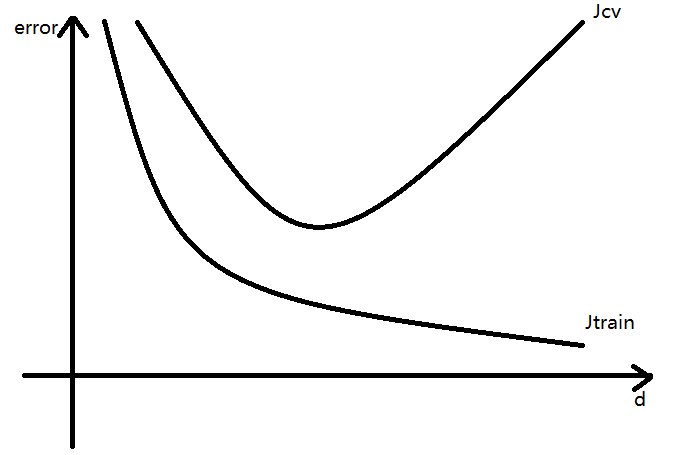

• 偏差问题
  当d比较小时，$J_cv$ 与 $J_trian$ 都很大，而且有 $J_cv \approx J_train$
  此时学习算法欠拟合，其偏差比较大
• 方差问题
  当d比较大时，$J_{train}$ 很小，且有 $J_cv >> J_train$
  此时学习算法过拟合，其方差比较大

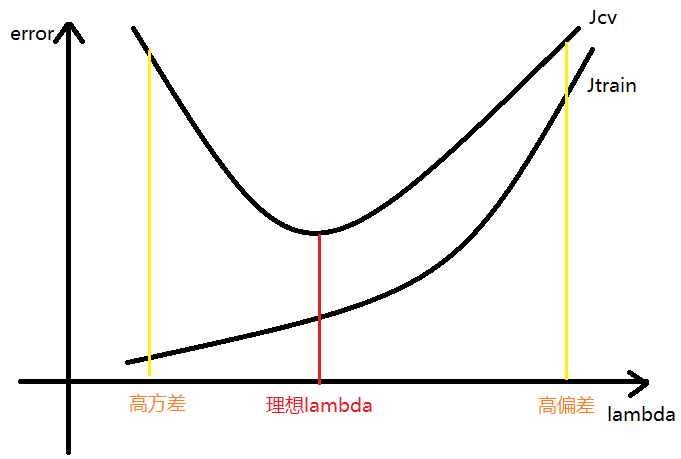
正则化参数的自动选择

正则化技术可以缓解过拟合问题；
选择不同的 $\lambda$ 的拟合结果——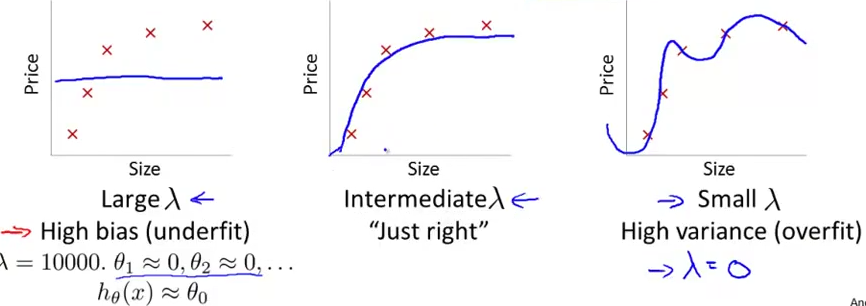

其参数 $\lambda$ 可以用交叉验证的方式逐一尝试并自动选择；

1. 选择某个 $\lambda_i$，最小化 $J_{train}(\theta)$ ，得到 $\theta^{(i)}$
   比如可以取 $\lambda = 0, 0.01, 0.02, 0.04, 0.08, …, 10.24, …$
2. 用交叉验证计算各组的 $J_{cv}(\theta^{(i)})$，选择使 $J_{cv}$ 最小的 $\lambda_i$
3. 使用参数 $\lambda_i$，利用测试集计算 $J_train(\theta)$ 检验算法的泛化能力

学习曲线Learning Curves

学习曲线描述 误差error 与 样本容量m 的关系——

• 存在偏差问题的学习曲线
  
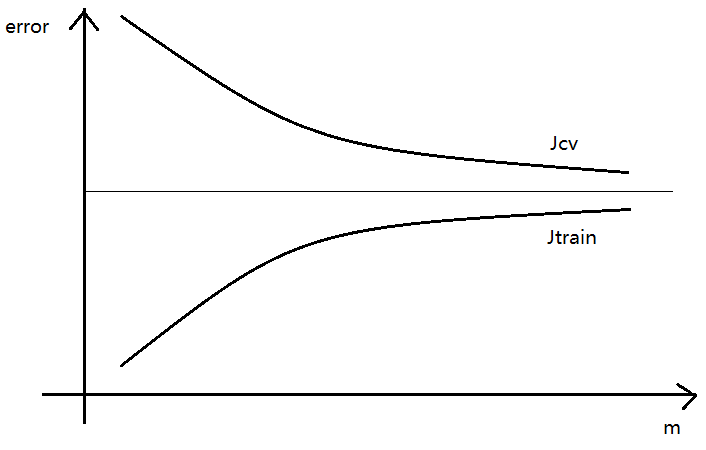
  当m比较大时，$J_{cv}$、$J_{train}$ 都比较高，而且两者不断接近；
  此时再增加训练样本对学习算法的提高没有太大的作用；
• 存在方差问题的学习曲线
  
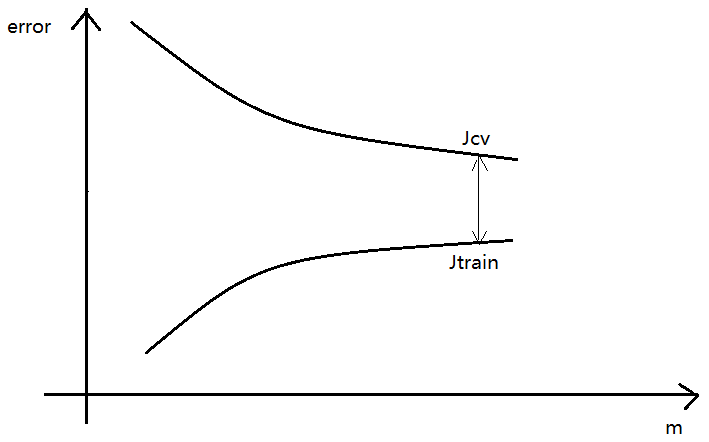
  当m比较大时，$J_{cv}$、$J_{train}$ 还是有比较大的差距；
  此时再增加训练样本对学习算法的提高还是有益的

神经网络

• 小型 & 大型
  对于小型神经网络，容易发生欠拟合现象，但计算量小；
  对于大型神经网络，容易发生过拟合现象，且计算量大；
  在计算能力足够的情况下，通常使用相对比较大型的神经网络，用正则化技术来缓解过拟合现象
• 神经网络的层数、隐藏层的神经元个数可以通过交叉验证的方式来选择

改进方向的选择

通过绘制学习曲线的方式判断当前算法存在偏差问题还是方差问题；

• 对于高偏差问题
  • 扩大特征集
  • 增加多项式特征
  • 减小$\lambda$
• 对于高方差问题
  • 增加训练样本
  • 精简特征集
  • 增大$\lambda$