吴恩达《机器学习》笔记

过拟合

过拟合是指学习器千方百计地逼近训练集导致不能很好的进行泛化
如下两图，分别是回归问题和分类问题的欠拟合、恰好拟合、过拟合的几种表现——

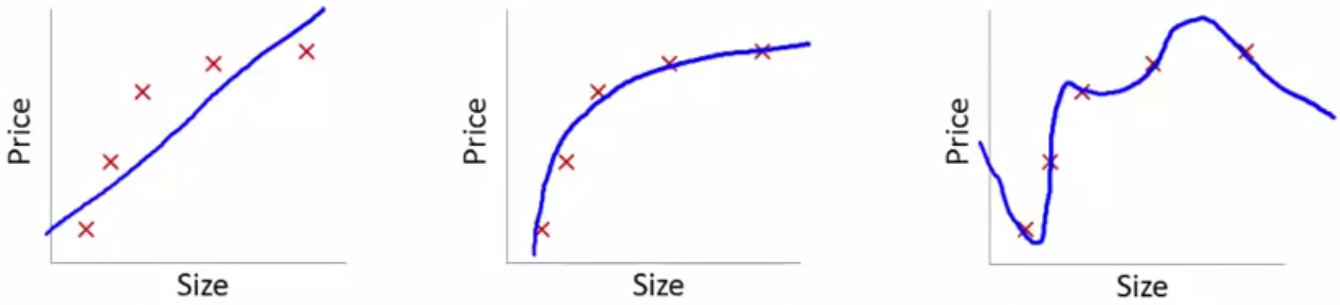
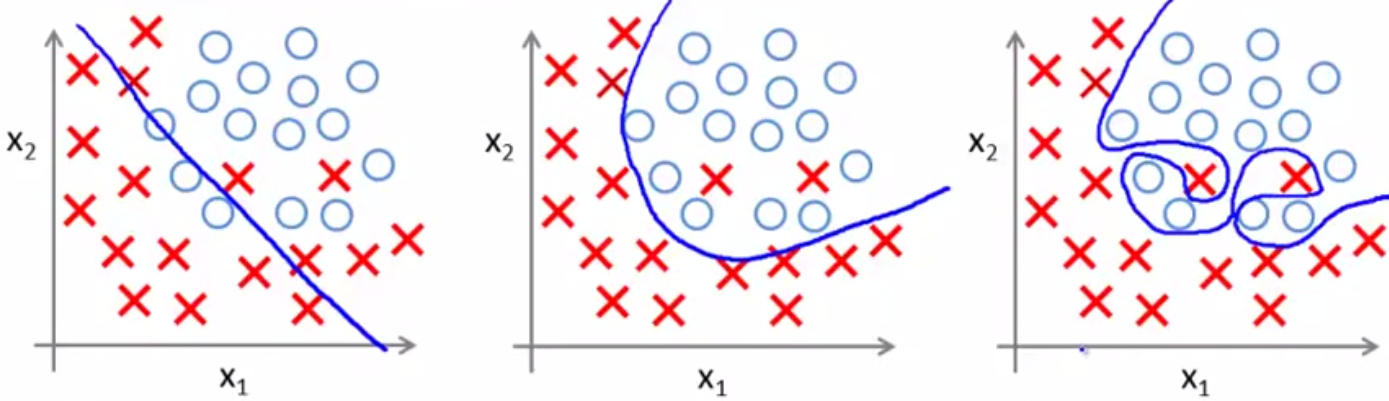
解决方法：

1. 减少特征数量
   • 手工选择
   • 模型选择算法：自动去除不必要的特征
2. 正则化
   保留特征，但减小参数

正则化

成本函数

• 原始的成本函数
  $$J(\theta) = \frac{1}{2m} \sum_{i=1}^{m} ( h_\theta(x^{(i)}) - y^{(i)} )^2$$

• 使用正则化技术的成本函数
  $$J(\theta) = \frac{1}{2m} [ \sum_{i=1}^{m} ( h_\theta(x^{(i)}) - y^{(i)} )^2 + \lambda \sum_{j=1}^{n} \theta_j^2 ]$$
  其中

  • $\lambda$ 为正则化参数

  • $\lambda \sum_{j=1}^{n} \theta_j^2$ 为正则化项
    用于惩罚参数，为了使J最小化，那么参数也要尽可能小，$\lambda$越大，惩罚的力度也就越大；
    这里只惩罚$\theta_1$到$\theta_n$，不考虑$\theta_0$，因为$\theta_0$对最终结果影响不大

    引入正则化项的目的是平衡“拟合训练目标”和“保持参数较小”两个目标
    当$\lambda$很大时，$\theta_j \approx 0$

牛顿法

• 原始方式
  $$
  \begin{aligned}
  重复直到收敛\{\\
  \theta_j :&= \theta_j - \alpha \sum_{i=1}^{m} \frac{\partial}{\partial \theta_j} J(\theta) \\
  &=\theta_j - \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} （所有\theta_j同时更新）\\
  \}
  \end{aligned}
  $$
• 正则化
  $$
  \begin{aligned}
  重复直到收敛\{\\
  \theta_0 :&= \theta_0 - \alpha \frac{1}{m} (h_\theta(x^{(i)}) - y^{(i)}) x_0^{(i)}\\
  \theta_j :&= \theta_j - \alpha \sum_{i=1}^{m} \frac{\partial}{\partial \theta_j} J(\theta)\\
  &=\theta_j - \alpha [ \frac{1}{m} \sum_{i=1}^{m} ( h_\theta(x^{(i)}) - y^{(i)} ) x_i^{(i)} + \frac{\lambda}{m} \theta_j ]\\
  &=\theta_j \underbrace{ (1-\alpha \frac{\lambda}{m}) }_{\text{略小于1，每次迭代都略微压缩参数}}
  -\underbrace{ \alpha \frac{1}{m} \sum_{i=1}^{m} (h_\theta(x^{(i)}) - y^{(i)}) x_j^{(i)} }_{\text{与原始的迭代公式的第二项一致}}\\
  &（所有\theta_j同时更新，且这里j>=1）\\
  \}
  \end{aligned}
  $$

正规方程法

• 原始方式
  $$\theta = (X^T X)^{-1}X^T y$$
• 正则化（推导略）
  $$\theta = (X^T X + \lambda M)^{-1}X^T y$$
  其中，
  $$M =
  \left( \begin{array}{ccc}
  0 & 0 & 0 & 0 & \ldots & 0 \\\
  0 & 1 & 0 & 0 & \ldots & 0 \\\
  0 & 0 & 1 & 0 & \ldots & 0 \\\
  0 & 0 & 0 & 1 & \ldots & 0 \\\
  \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\\
  0 & 0 & 0 & 0 & \ldots & 1 \\\
  \end{array} \right)
  $$
• 不可逆问题
  原始方式存在$X^T X$不可逆的问题，尽管可以求伪逆，但并不能得到很好的假设；
  正则化后，$X^T X + \lambda M$必定可逆（推导略）

优点

• 避免过拟合
  在完成拟合训练目标的同时，又保证了较小的参数
• 解决了不可逆问题
  即使特征很多而数据量较小的情况下仍能够顺利完成回归任务