我们通常称呼一维张量为“向量”，用一条线来抽象它；称呼二维张量为“矩阵”，用一个平面来抽象它；而三维张量也可以用一个立方体来抽象它——我们所生活的世界是一个三维的世界，理解一维、二维、三维的对象自然是得心应手，但有时候也不得不面对更加高维的数据结构，这时候该怎么理解它们呢？本文将试图从嵌套的角度入手，用低维张量嵌套的形式来辅助理解高维张量。

C语言的数组

众所周知，内存的排列是一维的，C语言本身也不存在真实的高维数组，我们通常用“数组的数组”这种形式来描述一个高维的数组。比如

• int a[2]定义了两个元素，它们组成一个数组a，也可以看成一个向量；
• int b[3][2]定义了三个数组组成了一个“数组的数组”b，这里的b可以看成一个矩阵；
• 同理，int c[4][3][2]就可以看成一个三维的张量

用低维张量嵌套定义高维张量

事实上，C语言的高维数组定义方式是一种嵌套定义——
记将元素排列组成数组的操作为$\alpha$，那么对于元素$a_1$, $a_2$，$A = \alpha (a_1, a_2)$就组成了一个数组；
如果把A看作元素，那么$\alpha(A_1, A_2) = \alpha(\alpha(a_{11}, a{12}), \alpha(a_{21}, a_{22}))$就以嵌套的形式构成了一个二维数组也即矩阵。

我们再用图片来描述这种嵌套过程：

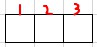
• 一维张量【$3$】
  
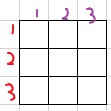
• 一维张量嵌套得到二维张量【$3 \times 3$】
  
• 二维张量（行先序）【$3 \times 3$】
  
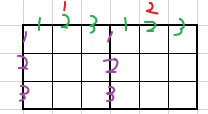
• 用一维嵌套二维张量得到三维张量【$2 \times 3 \times 3$】
  
• 用二维嵌套一维张量得到三维张量【$3 \times 3 \times 2$】
  
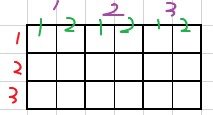
• 用二维嵌套二维张量得到四维张量【$2 \times 2 \times 3 \times 3$】
  

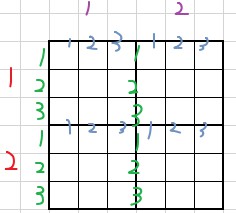
依次类推，我们甚至可以用更复杂的嵌套（比如对二维张量做两次二维嵌套得到六维张量），更高的基本维度（比如对三维张量做一维嵌套得到四维张量——卷积核的常用描述形式）。

《Winograd卷积原理 | Hey~YaHei!》一文中，二维Winograd的实现也正是这种嵌套思想推导出来的。