浅探Winograd量化
上一篇文章《Winograd卷积原理 | Hey~YaHei!》已经介绍过Winograd卷积的基本原理,但终究是理论上的推导,在实际应用的时候其实有些耐人寻味的地方:数学推导假设的是无限的精度和数值范围,但实际计算机的运算精度与数值范围都是有限的,不过按照论文《Fast algorithms for convolutional neural(CVPR2016)》的报告,Winograd在浮点运算上的表现都不错:
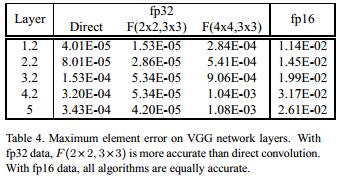
- $F(2\times2,3\times3)$的fp32精度损失甚至比Direct Convolution还小,这主要得益于乘法次数的减少,以及简单的变换矩阵(没有非常大或者非常小的数值)
- $F(4\times4,3\times3)$的fp32精度损失就比较大了,但似乎也还能接受
- fp16精度损失这三者表现的差不多
浮点运算的Winograd确实不错,但它却似乎也没那么轻易能套上量化——整型可没有浮点这么大的动态范围,如何保证运算过程整型不会溢出将是个令人头疼的问题。
溢出
假设将网络量化成int8,int8的权重和int8的输入,那么得益于int8 * int8,无论是Direct Convolution还是im2col+GEMM,这都能带来可观的加速。但在Winograd里可就不是这么回事了!
注意:im2col也没有对数值的大小进行变换
$F(2,3)$
回顾一下$F(2,3)$的变换矩阵:
$$
B^{T}=\left[\begin{array}{rrrr}{1} & {0} & {-1} & {0} \\ {0} & {1} & {1} & {0} \\ {0} & {-1} & {1} & {0} \\ {0} & {1} & {0} & {-1}\end{array}\right],
G=\left[\begin{array}{rrr}{1} & {0} & {0} \\ {\frac{1}{2}} & {\frac{1}{2}} & {\frac{1}{2}} \\ {\frac{1}{2}} & {-\frac{1}{2}} & {\frac{1}{2}} \\ {0} & {0} & {1}\end{array}\right],
A^{T}=\left[\begin{array}{rrrr}{1} & {1} & {1} & {0} \\ {0} & {1} & {-1} & {-1}\end{array}\right]
$$
$$
g=\left[\begin{array}{lll}{g_{0}} & {g_{1}} & {g_{2}}\end{array}\right]^{T},
d=\left[\begin{array}{llll}{d_{0}} & {d_{1}} & {d_{2}} & {d_{3}}\end{array}\right]^{T}
$$
接下来计算一下$U$矩阵和$V$矩阵:
from sympy import Matrix, Symbol
BT = Matrix([
[1, 0, -1, 0],
[0, 1, 1, 0],
[0, -1, 1, 0],
[0, 1, 0, -1]
])
G = Matrix([
[2, 0, 0],
[1, 1, 1],
[1, -1, 1],
[0, 0, 2]
])
AT = Matrix([
[1, 1, 1, 0],
[0, 1, -1, -1]
])
g = Matrix([[Symbol('g0')], [Symbol('g1')], [Symbol('g2')]])
d = Matrix([[Symbol('d0')], [Symbol('d1')], [Symbol('d2')], [Symbol('d3')]])
m = Matrix([[Symbol('m0')], [Symbol('m1')], [Symbol('m2')], [Symbol('m3')]])
print("G * g:", G * g)
print("BT * d:", BT * d)
print("AT * m:", AT * m)
$$
Gg = \left[\begin{array}{l}{2g_0} & {g_0+g_1+g_2} & {g0-g1+g2} & {2g_2}\end{array}\right]^T
\\
B^Td = \left[\begin{array}{l}{d_0-d_2} & {d_1+d_2} & {-d_1+d_2} & {d_1-d_3}\end{array}\right]^T
\\
\frac{1}{2} A^Tm = \frac{1}{2} \left[\begin{array}{l}{m_0+m_1+m_2} & {m_1-m_2-m_3}\end{array}\right]^T
$$
输入、输出变换过程包含8次加法和2次移位;
同时可以看到,为了保证计算不溢出,$Gg$需要额外的2个bits,而$B^Td$需要额外的1个bit,换言之,为了保证安全的int8 * int8,权重和输入分别得量化到int6和int7。
$F(2\times2,3\times3)$
g = Matrix(3, 3, [Symbol(f'g{i}') for i in range(3*3)])
d = Matrix(4, 4, [Symbol(f'd{i}') for i in range(4*4)])
m = Matrix(4, 4, [Symbol(f'm{i}') for i in range(4*4)])
print("G * g * GT:", G * g * G.T)
>>> Matrix([
... [ 4*g0, 2*g0 + 2*g1 + 2*g2, 2*g0 - 2*g1 + 2*g2, 4*g2],
... [2*g0 + 2*g3 + 2*g6, g0 + g1 + g2 + g3 + g4 + g5 + g6 + g7 + g8, g0 - g1 + g2 + g3 - g4 + g5 + g6 - g7 + g8, 2*g2 + 2*g5 + 2*g8],
... [2*g0 - 2*g3 + 2*g6, g0 + g1 + g2 - g3 - g4 - g5 + g6 + g7 + g8, g0 - g1 + g2 - g3 + g4 - g5 + g6 - g7 + g8, 2*g2 - 2*g5 + 2*g8],
... [ 4*g6, 2*g6 + 2*g7 + 2*g8, 2*g6 - 2*g7 + 2*g8, 4*g8]])
print("BT * d * B:", BT * d * BT.T)
>>> Matrix([
... [ d0 + d10 - d2 - d8, d1 - d10 + d2 - d9, -d1 - d10 + d2 + d9, d1 + d11 - d3 - d9],
... [ -d10 + d4 - d6 + d8, d10 + d5 + d6 + d9, d10 - d5 + d6 - d9, -d11 + d5 - d7 + d9],
... [ -d10 - d4 + d6 + d8, d10 - d5 - d6 + d9, d10 + d5 - d6 - d9, -d11 - d5 + d7 + d9],
... [-d12 + d14 + d4 - d6, -d13 - d14 + d5 + d6, d13 - d14 - d5 + d6, -d13 + d15 + d5 - d7]])
print("AT * m * A:", AT * m * AT.T)
>>> Matrix([
... [ m0 + m1 + m10 + m2 + m4 + m5 + m6 + m8 + m9, m1 - m10 - m11 - m2 - m3 + m5 - m6 - m7 + m9],
... [-m10 - m12 - m13 - m14 + m4 + m5 + m6 - m8 - m9, m10 + m11 - m13 + m14 + m15 + m5 - m6 - m7 - m9]])
输出矩阵的各元素系数绝对值之和$\mu(\cdot)$:
$$
\mu(GgG^T) = \left[\begin{array}{llll}
{4} & {6} & {6} & {4} \\
{6} & {9} & {9} & {6} \\
{6} & {9} & {9} & {6} \\
{4} & {6} & {6} & {4}
\end{array}\right],
\mu(B^TdB) = \left[\begin{array}{llll}
{4} & {4} & {4} & {4} \\
{4} & {4} & {4} & {4} \\
{4} & {4} & {4} & {4} \\
{4} & {4} & {4} & {4}
\end{array}\right]
$$
输入、输出变换过程包含80次加法和4次移位($\frac{1}{4}A^TmA$);
同时可以看到,为了保证计算不溢出,$GgG^T$需要额外的4个bits,而$B^TdB$需要额外的2个bit,换言之,为了保证安全的int8 * int8,权重和输入分别得量化到int4和int6。
$F(4\times4,3\times3)$
$$
B^{T}=\left[\begin{array}{rrrrrr}
{4} & {0} & {-5} & {0} & {1} & {0} \\
{0} & {-4} & {-4} & {1} & {1} & {0} \\
{0} & {4} & {-4} & {-1} & {1} & {0} \\
{0} & {-2} & {-1} & {2} & {1} & {0} \\
{0} & {2} & {-1} & {-2} & {1} & {0} \\
{0} & {4} & {0} & {-5} & {0} & {1}
\end{array}\right],
G=\left[\begin{array}{rrr}
{6} & {0} & {0} \\
{-4} & {-4} & {-4} \\
{-4} & {4} & {-4} \\
{1} & {2} & {4} \\
{1} & {-2} & {4} \\
{0} & {0} & {24}
\end{array}\right]
$$
为了保证计算不溢出,$GgG^T$需要额外的10个bits($G$最后一行绝对值之和最大,$24^2=576$),而$B^TdB$需要额外的7个bits($B^T$最后一行的绝对值之和最大,$10^2=100$),换言之……压根没法保证int8 * int8的安全计算。这时候可能只能将int8扩展到int16,执行int16 * int16的乘法运算,即便如此,权重也只能量化到int6.
大家是怎么做的?
ncnn和mnn的量化计算本质上是int16 * int16而非int8 * int8,所以$F(2\times2,3\times3)$完全没有溢出的问题,而$F(4\times4,3\times3)$需要将权重量化到int6;Tengine的量化计算是int8 * int8,1.6版本已经支持Winograd卷积,但目前还没有支持Winograd量化。
思考:先变换后量化?
对量化的输入和权重做变换时溢出问题着实让人头疼,既然如此,我们能不能先做变换再进行量化呢?
不过,要是先变换再量化,乘出来之后就反量化不回去了QAQ
更快的变换
上一篇文章我们已经提到过——
尽管$V = B^{T} d B$和$Y = A^T M A$的计算过程中也有大量的乘法,但观察可以发现$F(4,3)$和$F(6,3)$的$A^T$矩阵和$B^T$中有相当多的元素恰好是$2^n$,也就是说,用Winograd计算量化的卷积应该会有神奇的加成
现在我们来看看具体有哪些神奇的变化:
from math import log2
def _op_count(sym_matrix):
adds, shifts, muls = 0, 0, 0
abs_v_pool = []
for elem in sym_matrix:
d = elem.as_coefficients_dict()
adds += len(d) - 1
for v in d.values():
abs_v = abs(v)
if abs_v != 1 and abs_v not in abs_v_pool:
abs_v_pool.append(abs_v)
log = log2(abs_v)
if log == int(log):
shifts += 1
else:
muls += 1
return {"adds": adds, "shifts": shifts, "muls": muls}
def op_count_1D(M1, M2):
return _op_count(M1 * M2)
def op_count_2D(M1, M2):
t = M1 * M2
counter1 = _op_count(t)
M3 = Matrix(*t.shape, [Symbol(f't{i}') for i in range(len(t))])
counter2 = _op_count(M3 * M1.T)
return {
"adds": counter1['adds'] + counter2['adds'],
"shifts": counter1['shifts'] + counter2['shifts'],
"muls": counter1['muls'] + counter2['muls'],
}
print(op_count_1D(G, g))
print(op_count_1D(BT, d))
print(op_count_1D(AT, m))
print(op_count_2D(G, g))
print(op_count_2D(BT, d))
print(op_count_2D(AT, m))
将输入、输出变换过程中的大量乘法替换成移位运算之后,理论上Winograd能变得更快!
| Winograd | 原始乘法 | Win乘法 | Win量化乘法 | 理论加速比 | 含变换加速比 | 含变换加速比(量化) |
|---|---|---|---|---|---|---|
| $F(2,3)$ | 6 | 4(4) | 4(4) | 1.50 | 1.50 | 1.50 |
| $F(4,3)$ | 12 | 12(6) | 7(6) | 2.00 | 1.00 | 1.71 |
| $F(6,3)$ | 18 | 28(8) | 13(8) | 2.25 | 0.64 | 1.38 |
| 堆$F(2\times2,3\times3)$ | 36 | 24(24) | 24(24) | 1.50 | 1.50 | 1.50 |
| 堆$F(4\times4,3\times3)$ | 144 | 126(72) | 78(76) | 2.00 | 1.14 | 1.85 |
| 堆$F(6\times6,3\times3)$ | 324 | 396(144) | 184(144) | 2.25 | 0.82 | 1.76 |
| 嵌$F(2\times2,3\times3)$ | 36 | 16(16) | 16(16) | 2.25 | 2.25 | 2.25 |
| 嵌$F(4\times4,3\times3)$ | 144 | 48(36) | 38(36) | 4.00 | 3.00 | 3.79 |
| 嵌$F(6\times6,3\times3)$ | 324 | 102(64) | 74(64) | 5.06 | 3.12 | 4.38 |