线性量化
简单来说,量化就是将浮点存储(运算)转换为整型存储(运算)的一种模型压缩技术。如果按《当前深度神经网络模型压缩和加速都有哪些方法?-机器之心》一文的分类方式,量化属于参数共享的一种——将原始数据聚为若干类(比如int8量化为$2^8=256$类),量化后的整型值就相当于类的索引号。
按照聚类中心是否均匀分布,可以把量化分为线性量化和非线性量化。
- 如《Deep Compression: Compressing Deep Neural Networks with Pruning, Trained Quantization and Huffman Coding(2016)》就是典型的非线性量化,作者采用不规则的聚类中心,通过KMEANS对浮点权重进行量化,并在训练过程中逐步修正聚类中心——不规则的聚类中心往往能在相同的比特数下取得更小的量化误差,但由于必须先查表取得原始数据再进行计算,所以对计算的加速没有任何帮助,这种方法更多是用来压缩模型文件大小。
- 与非线性量化不同,线性量化采用均匀分布的聚类中心,原始数据跟量化后的数据存在一个简单的线性变换关系。而卷积、全连接本身也只是简单的线性计算,因此在线性量化中可以直接用量化后的数据进行直接计算,不仅可以压缩模型文件的大小,还能带来明显的速度提升。
动机
- 更少的存储开销和带宽需求
使用更少的比特数存储数据,有效减少应用对存储资源的依赖(但现代系统往往拥有相对丰富的存储资源,这一点已经不算是采用量化的主要动机) - 更快的计算速度
对多数处理器而言,整型运算的速度一般(但不总是)比浮点运算更快 - 更低的能耗与占用面积
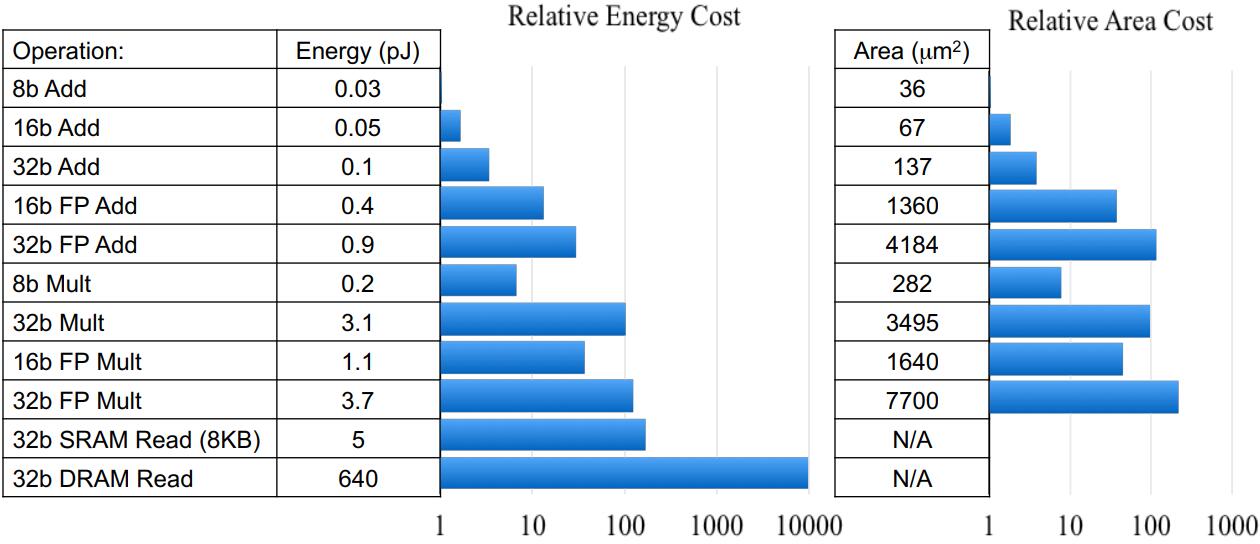
数据来源:《High-Performance Hardware for Machine Learning(NIPS2015)》
从上图可以看到,FP32乘法的能耗是INT8乘法能耗的18.5倍,芯片占用面积则是27.3倍——对芯片设计和FPGA设计而言,更少的资源占用意味着相同数量的单元下可以设计出更多的计算单元;而更少的能耗意味着更少的发热,和更长久的续航。 - 尚可接受的精度损失
量化相当于对模型权重引入噪声,所幸CNN本身对噪声不敏感(甚至在训练过程中,模拟量化所引入的权重加噪还有利于防止过拟合),在合适的比特数下量化后的模型并不会带来很严重的精度损失。按照gluoncv提供的报告,经过int8量化之后,ResNet50_v1和MobileNet1.0_v1在ILSVRC2012数据集上的准确率仅分别从77.36%、73.28%下降为76.86%、72.85%。 - 趋势
无论是移动端还是服务器端,都可以看到新的计算设备正不断迎合量化技术。比如NPU/APU/AIPU等基本都是支持int8(甚至更低精度的int4)计算的,并且有相当可观的TOPs,而Mali GPU开始引入int8 dot支持,Nvidia也不例外——
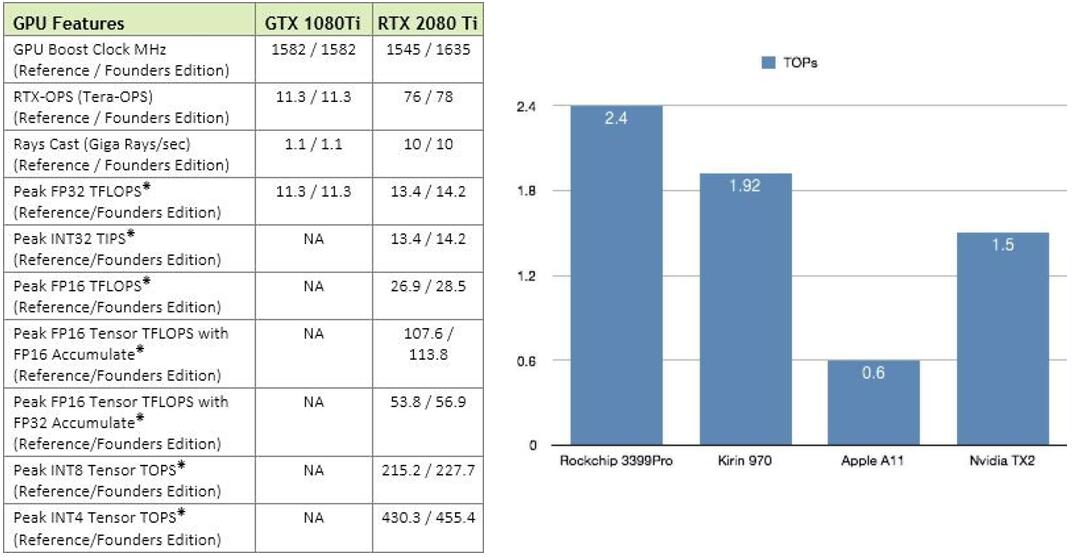
线性量化
常见的线性量化过程可以用以下数学表达式来表示:
$$r = Round(S(q - Z))$$
其中,
$q$ 是float32的原始值;
$Z$ 是float32的偏移量,也可以量化为int32;
$S$ 是float32的缩放因子;
$Round(\cdot)$ 是四舍五入近似取整的数学函数,除了四舍五入,向上、向下取整也是可以的;
$r$ 是量化后的一个整数值。
而我们需要做的,就是确定合适的 $S$ 和 $Z$
对称和非对称
参考:Algorithms - Quantization | Distiller
根据参数 $Z$ 是否为零可以将线性量化分为两类——对称和非对称。
对称量化
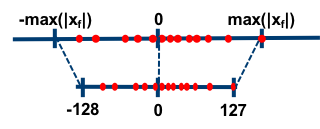
在对称量化中,$r$ 是用有符号的整型数值来表示的,此时 $Z=0$,且 $q=0$ 时恰好有 $r=0$。
比如简单地取,
$$S = \frac{2^{n-1} - 1}{max(|x|)}$$
$$Z = 0$$
其中,
$n$ 是用来表示该数值的位宽,
$x$ 是数据集的总体样本。对称量化比较简单,不仅实现简单,而且由于$Z=0$运算也变得非常简单。
非对称量化
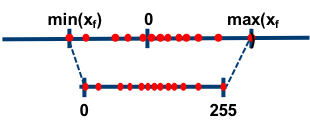
比如简单地取,
$$S = \frac{2^{n-1} - 1}{max(x)-min(x)}$$
$$Z = min(x)$$
非对称量化比较灵活,通常 $r$ 是用无符号的整型数值来表示,此时 $Z \neq 0$。
逐层、逐组和逐通道
按照量化的粒度(共享量化参数的范围)可以分为逐层、逐组和逐通道——
- 逐层量化以一个层为单位,整个layer的权重共用一组缩放因子$S$和偏移量$Z$;
- 逐组量化以组为单位,每个group使用一组$S$和$Z$;
- 逐通道量化则以通道为单位,每个channel单独使用一组$S$和$Z$。
当 $group=1$ 时,逐组量化与逐层量化等价;
当 $group=num\_filters$ (即dw卷积)时,逐组量化逐通道量化等价
在线和离线
按照激活值的量化方式,可以分为在线(online)量化和离线(offline)量化。
- 在线量化指激活值的 $S$ 和 $Z$ 在实际推断过程中根据实际的激活值动态计算;
- 离线量化指提前确定好激活值的 $S$ 和 $Z$
由于不需要动态计算量化参数,通常离线量化的推断速度更快些,通常有三种方法来确定相关的量化参数——
- 指数平滑平均
将校准数据集投喂给模型,收集每个量化的层的输出特征图,计算每个batch的 $S$ 和 $Z$,并通过指数平滑平均更新 $S$ 和 $Z$ - 直方图截断
以$S = \frac{2^n - 1}{max(|x|)}$为例,由于有的特征图会出现偏离较远的奇异值,导致max非常大,所以可以通过直方图截取的形式,比如抛弃最大的前1%数据,以前1%分界点的数值作为max计算量化参数 - KL散度校准
参考:《8-bit Inference with TensorRT》
TensorRT的校准方案,通过KL散度(也称为相对熵,用以描述两个分布之间的差异)来评估量化前后分布的差异,搜索并选取KL散度最小的量化参数
模拟量化实验
我在Gluon上用mobilenet和resnet50做了简单的模拟量化实验(量化卷积和全连接):Quantization.MXNet | github
| IN dtype | IN offline | WT dtype | WT qtype | Merge BN | w/o 1st conv | M-Top1 Acc | R-Top1 Acc |
|---|---|---|---|---|---|---|---|
| float32 | / | float32 | / | / | 73.28% | 77.36% | |
| uint8 | x | int8 | layer | 44.57% | 55.97% | ||
| uint8 | x | int8 | layer | √ | 70.84% | 76.92% | |
| uint8 | naive | int8 | layer | √ | 70.92% | 76.90% | |
| uint8 | KL | int8 | layer | √ | 70.72% | 77.00% | |
| int8 | naive | int8 | layer | √ | 70.58% | 76.81% | |
| int8 | KL | int8 | layer | √ | 70.66% | 76.71% | |
| int8 | x | int8 | layer | √ | √ | 15.21% | 76.62% |
| int8 | naive | int8 | layer | √ | √ | 32.70% | 76.61% |
| int8 | KL | int8 | layer | √ | √ | 14.70% | 76.60% |
| uint8 | x | int8 | channel | 47.80% | 56.21% | ||
| uint8 | x | int8 | channel | √ | 72.93% | 77.33% | |
| uint8 | naive | int8 | channel | √ | 72.85% | 77.31% | |
| uint8 | KL | int8 | channel | √ | 72.68% | 77.35% | |
| int8 | naive | int8 | channel | √ | 72.63% | 77.22% | |
| int8 | KL | int8 | channel | √ | 72.68% | 77.08% | |
| int8 | x | int8 | channel | √ | √ | 72.75% | 77.11% |
| int8 | naive | int8 | channel | √ | √ | 72.04% | 76.69% |
| int8 | KL | int8 | channel | √ | √ | 72.67% | 77.07% |
- 由于大部分网络使用relu作为激活函数,所以往往使用uint能获得更小的量化误差,不过也有的平台只支持int8的量化(比如ncnn);
- 离线量化的校准数据集从训练集抽取(每个类别抽取5张图片,共计5000张),naive校准采用指数平滑平均的方式收集最大值并计算量化参数,KL校准搜索KL散度最小的量化参数;
- 由于合并BN层后,不同通道的权重的分布差异变得更加显著,这对冗余网络(如resnet)跟逐通道量化的影响较小,但逐层量化紧凑网络(如mobilent)就直接崩溃(对dw卷积影响显著);
- 大部分情况下naive校准和KL校准效果都挺接近,不过在合并BN后的逐通道量化下,KL校准则明显由于naive校准;
为了进一步比较naive校准和KL校准,在cifar_resnet56_v1模型上又补充了几个简单实验:
| IN dtype | WT dtype | WT qtype | Merge BN | w/o 1st conv | Top1 Acc@naive | Top1 Acc@KL |
|---|---|---|---|---|---|---|
| float32 | float32 | / | / | 93.60% | 93.60% | |
| uint6 | int6 | channel | √ | √ | 93.09% | 93.83% |
| uint5 | int5 | channel | √ | √ | 92.71% | 93.29% |
| uint4 | int4 | channel | √ | √ | 91.62% | 89.27% |
| uint3 | int3 | channel | √ | √ | 81.75% | 55.98% |
可以看到,
- 在比特数还比较高(量化误差比较小)的情况下,KL校准明显优于naive校准;
- 但当比特数比较低的时候(量化误差变大)的情况下,KL校准的优势逐渐缩小,甚至最后崩溃
重训练量化实验
当量化的比特数比较大的情况下(如8bits),逐通道量化、KL校准已经能取得很不错的效果;但当比特数非常小的时候,量化带来的精度损失还是比较明显的,此时我们可以按照《Quantization and Training of Neural Networks for Efficient Integer-Arithmetic-Only Inference(2017)》做简单的恢复训练:Quantization.MXNet | github
BN层的处理:
通常我们会把训练好的模型的BN层融合到卷积层当中来减少推断时间,量化卷积权重之前也需要先把BN层融合进去,但是在训练过程中我们又需要BN层来抑制过拟合,那么可以在训练过程中引入伪BN——
正常的BN是对卷积的输出特征图进行操作,而按照合并BN的思路,伪BN则是直接对权重进行操作。先用BN的参数与原始权重进行计算取得“融合”后的权重,再用新的权重进行卷积,在训练过程中正常更新原始的卷积权重和BN的参数。
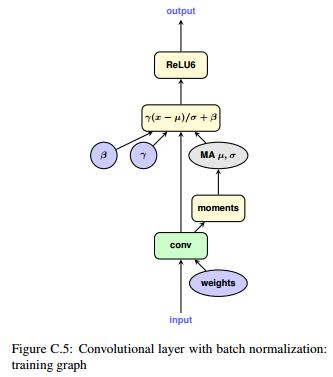
使用伪BN后,每次前向传播需要两次卷积运算——
- 用原始权重卷积,卷积输出用于更新伪BatchNorm的平均值、标准差,这次卷积运算不需要反向传播;
- 另外一次用量化过的权重卷积,卷积输出的结果作为下一层的输入,这一次的卷积运算需要反向传播
这样一来,训练的速度会明显降低,但却保留的BN本身的效果。
4bits量化的恢复训练效果如下:
| DataType | QuantType | Offline | Retrain | FakeBN | Top-1 Acc |
|---|---|---|---|---|---|
| fp32/fp32 | / | / | / | / | 93.60% |
| uint4/int4 | layer | naive | √ | 84.95% | |
| uint4/int4 | layer | KL | √ | 73.36% | |
| uint4/int4 | layer | √ | √ | √ | 90.77% |
| uint4/int4 | channel | naive | √ | 91.62% | |
| uint4/int4 | channel | KL | √ | 89.27% | |
| uint4/int4 | channel | √ | √ | √ | 93.19% |
- 由于比特数较低,KL校准的效果变得非常差;
- 相比于naive校准,恢复训练总能取得更低一些的精度损失