漫谈池化层
BGM:《革命机valvrave》ED1
有点小high,建议先调低音量再播放;
还有个现场版,像是中二版的凤凰传奇hhhhh——TMRevolution×水樹奈々 - Preserved Roses_革命デュアリズム_ | bilibili
话说水树奈奈是不是有点像隔壁控制学院的ly哈?
不过现场版的调音好像有问题,重低音效果有点差~
参考:
- 《Hands-On Machine Learning with Scikit-Learn and TensorFlow(2017)》Chap13
《Hands-On Machine Learning with Scikit-Learn and TensorFlow》笔记 - 《卷积神经网络——深度学习实践手册(2017.05)》
- 《Deep Learning 深度学习(2017)》
基本的池化操作
简单的聚合操作,取均值、取最值等,分别称为平均池化(Average Pooling)和最大池化(Max Pooling);
一般使池化核的大小与步长相等,不重叠、全覆盖地进行降采样;
平均池化和最大池化的tensorflow实现参见 卷积神经网络CNN / tensorflow实现 / 池化层 | Hey~YaHei!
池化的意义
既对数据进行降采样(down-sampling)操作,又可以用p范数(p-norm)作非线性映射的“卷积”
$$p范数:||A||_p = (\sum_{i=1}^m \sum_{j=1}^n |a_{ij}|^p)^{1/p}, p>=1$$
当 $p \to \infty$ 时即为最大池化
具体作用为:
- 特征不变性
使模型更关注包含一定的自由度,能容忍特征微小的位移 - 特征降维
降采样使后续操作的计算量得到减少 - 一定程度防止过拟合
平均池化和最大池化的区别
论文 Learning Mid-Level Features For Recognition(2010) 第5节
CNN特征提取的误差主要来自两个方面:
- 邻域大小受限造成的估计值方差增大
平均池化能有效减少该误差,更多的保留图像的背景信息;
均匀采样的方差只有总体方差的 $\frac{1}{N}$;
但如果模型中杂波方差较大(也即第二个误差明显),最后输出类别的概率分布将出现明显的混叠,导致分类准确率下降 - 卷积层参数误差造成估计值均值偏移
最大池化能有效减少该误差,更多的保留图像纹理信息;
最大值采样的方差为总体方差的 $\frac{1}{\sqrt{log(N)}}$ (推导过程参见论文),受第一种误差影响较大;
改进的池化操作
重叠池化(Overlapping Pooling)
论文:ImageNet Classification with Deep Convolutional Neural Networks(2012) 第3.4节——
3.4 Overlapping Pooling
Pooling layers in CNNs summarize the outputs of neighboring groups of neurons in the same kernel map. Traditionally, the neighborhoods summarized by adjacent pooling units do not overlap (e.g., [17, 11, 4]). To be more precise, a pooling layer can be thought of as consisting of a grid of pooling units spaced s pixels apart, each summarizing a neighborhood of size z × z centered at the location of the pooling unit. If we set s = z, we obtain traditional local pooling as commonly employed in CNNs. If we set s < z, we obtain overlapping pooling. This is what we use throughout our network, with s = 2 and z = 3. This scheme reduces the top-1 and top-5 error rates by 0.4% and 0.3%, respectively, as compared with the non-overlapping scheme s = 2; z = 2, which produces output of equivalent dimensions. We generally observe during training that models with overlapping pooling find it slightly more difficult to overfit.
卧槽,这篇论文居然有1.3万的被引?!?!?!?
思路很简单,让池化的步长略小于池化核的大小,使相邻的池化图像块出现一定程度的重叠;
据论文介绍,相比于大小2x2、步长2的传统池化操作,3x3、步长2的重叠池化操作使他们的模型的分类错误率top-1和top-5分别降低0.4%和0.3%;
并且他们通过实验观察到(有点主观),重叠池化具有一定的正则化作用;
随机池化(Stochastic Pooling)
论文:Stochastic Pooling for Regularization of Deep Convolutional Neural Networks(2013)
按一定概率随机选取其中一个元素,介于平均池化和最大池化之间,并且受dropout启发,具有更好的正则化效果;
可以看作是,在输入图片的许多副本(有一些小的局部变形)上进行标准的最大池化操作;
具体操作
- 训练(随机采样)
- 归一化卷积层的输出计算,并以此作为每个元素的概率
$$ p_i = \frac{a_i}{\sum_{k \in R_j} a_k} $$
其中,
$p_i$ 是第i个输出的采样概率,
$a_i$ 是前层(卷积层)的第i个输出,
$R_j$ 是池化核扫过的第j个区域 - 用基于概率 $p$ 的多项分布的随机数对池化核扫过的区域进行随机采样作为区域池化的输出
$$ s_j = a_l \text{ where } l~P(p_1, …, p_{|R_j|}) $$
其中,
$s_j$ 是第j个区域的输出,
$a_l$ 是随机采样抽中的前层的一个输出 - 反向传播时,将抽中的元素用于梯度计算
- 归一化卷积层的输出计算,并以此作为每个元素的概率
- 预测(加权平均)
$$ s_j = \sum_{i \in R_j} p_i a_i $$
依旧计算每个前层输出的概率,以概率为权重,对池化核扫过的区域内每个输出作加权平均作为区域的输出
分析比较
- 与最大池化相比(主要体现在训练上)
最大池化仅仅保留区域内的最大值;而随机池化以各元素值的大小为概率,使非最大值的元素也有一定概率参与训练 - 与平均池化相比(主要体现在预测上)
平均池化不考虑权重,直接对区域内元素作算术平均;而随机池化采用加权平均,经过实验可以得知相对于平均池化有比较大的提升 - 与dropout相比
同样在训练中产生了很多不同的模型;
考虑包含n个大小为d的区域的随机池化,其产生的可能模型有 $n^d$ 种,其中d通常为 $10^4 - 10^6$,且n通常取 $4, 9, 16$(相比之下,dropout中 $n=2$,因为只有激活/失活两种状态);
再者,dropout似乎不适宜用于卷积层,而随机池化可以;
实验比较
- 准确度
根据论文,相比于最大池化、平均池化、dropout,随机池化在CIFAR-10、MNIST、CIFAR-100、SVHN数据集上都取得比较明显的提升 - 数据集规模
论文以MNIST、CIFAR-10数据集为例,随机抽取数据集的子集对不同池化操作进行比较,如下图所示(左MNIST,右CIFAR-10):
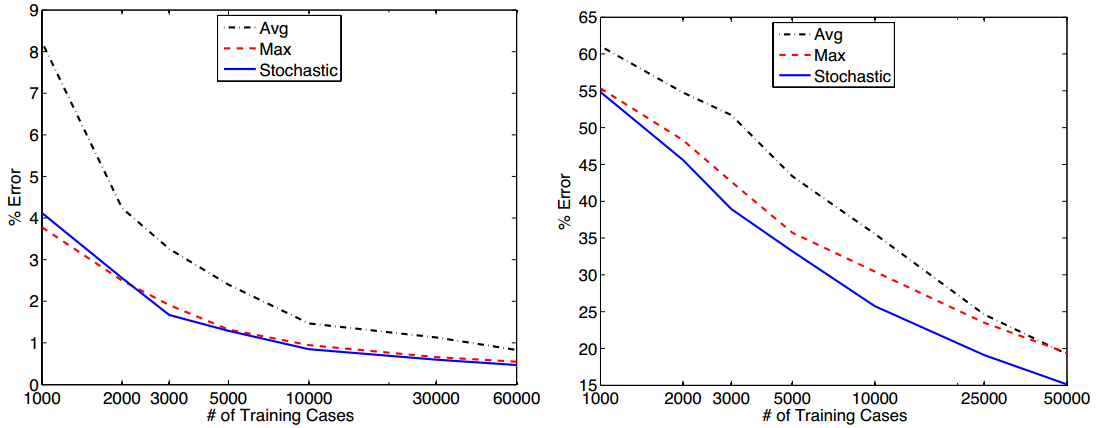
- 数据集很小时,随机池化与最大池化效果相当,平均池化效果明显要差一些;
- 随着数据集增大,随机池化与最大池化的效果几乎一直比平均池化要好(CIFAR-10在数据集比较大时,平均池化和最大池化效果相当);
- 随着数据集增大,随机池化与平均池化在MNIST上表现相当;在CIFAR-10上表现更优
- 不同训练、预测操作的组合
论文以CIFAR-10数据集为例,对不同的池化方式在训练、预测上的不同组合进行比较,如下图所示:
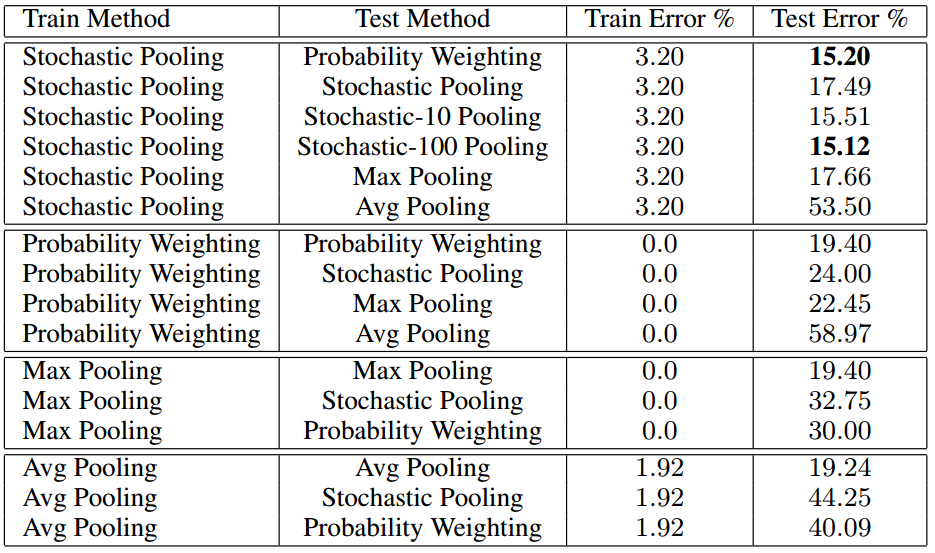
可以看到,随机池化训练 + 加权平均预测 是最佳组合方式 - 网络输出可视化
作者用反卷积技术对网络输出进行可视化,以此比较最大池化、平均池化、随机池化以及训练过程中使用多项分布抽样、均匀抽样的不同表现;
如下图所示(FF、UN分别表示多项分布抽样、均匀分布抽样的随机池化):

可以看到,最大池化可以比较好的保留图片中的纹理信息,而平均池化已经失去可辨识的纹理信息了;
多项分布抽样的随机池化表现良好,甚至比最大池化保留更多的纹理信息;
随着更多的FF被替换为UN,纹理信息逐步丧失,而且越靠近底层的随机池化影响越严重;
空间金字塔池化(Spatial Pyramid Pooling, SPP)
论文:Spatial Pyramid Pooling in Deep Convolutional Networks for Visual Recognition(2015)
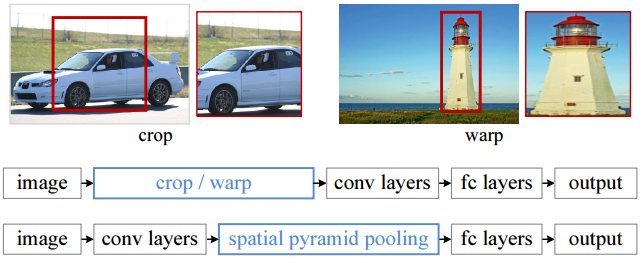
传统CNN中,输入的图片数据必须是特定尺度的,以确保进入FC或SVM前的尺寸固定(连接矩阵的大小固定);
因而往往在输入数据前需要对图片进行尺寸处理,比如裁剪、缩放;
而SPP操作不仅可以支持多尺度的图片输入,而且多方面特征提取更具鲁棒性,在目标检测任务上能够明显提高精度;
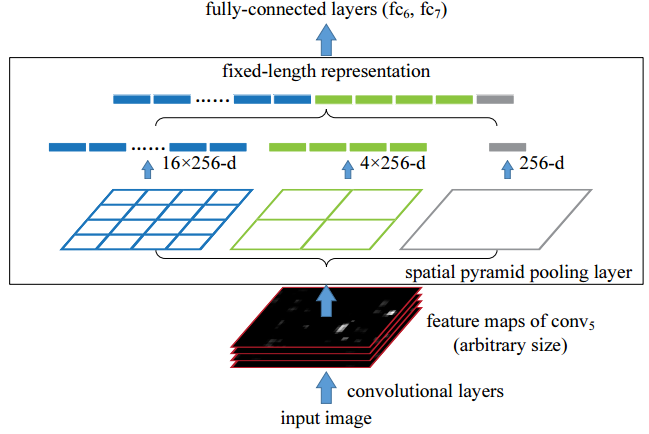
convolutional layers包含卷积、激活函数、池化操作,假设最后一层输出 $N_f$ 个 $a \times b$的特征图
论文中假设 $N_f = 256, a = b = 13$spatial pyramid pooling layers是一个典型三层SPP,包含三组动态参数(核大小、步长由 $a$ 和 $b$ 决定)的最大池化操作
这里的池化都是不padding、允许重叠的- 第一组(最右)为每个特征图生成一个1x1的池化图
换言之,采用核大小为 $a \times b$ 、步长为 $[a, b]$ 的最大池化 - 第二组(中间)为每个特征图生成一个2x2的池化图
换言之,采用核大小为 $\lceil a/2 \rceil \times \lceil b/2 \rceil$、步长为 $\lfloor a/2 \rfloor, \lfloor b/2 \rfloor$ 的最大池化 - 第三组(最左)为每个特征图生成一个4x4的池化图
换言之,采用核大小为 $\lceil a/4 \rceil \times \lceil b/4 \rceil$、步长为 $\lfloor a/4 \rfloor, \lfloor b/4 \rfloor$ 的最大池化 - 最后将三组池化图展开拼接起来,得到一个 $(1+4+16) \times N_f$ 的固定大小输出
注意到这里的N是由最后一个卷积层的参数之一,也就是一个网络超参数,不受输入数据的大小影响
- 第一组(最右)为每个特征图生成一个1x1的池化图
- 最后跟常规操作相同,将SSP的输出展平之后接FC
比如论文中的fc6的大小为4096
tensorflow实现:
参考 深度学习中空间金字塔池化的TensorFlow实现 | 百度百家号
def spp_layer(self, input_, levels=[2, 1], name = 'SPP_layer'):
'''Multiple Level SPP layer. Works for levels=[1, 2, 3, 6].'''
shape = input_.get_shape().as_list()
with tf.variable_scope(name):
pool_outputs = []
for l in levels:
# 计算池化核大小
kernel_size = [
1, # batch
np.ceil(shape[1] * 1. / l).astype(np.int32), # row
np.ceil(shape[2] * 1. / l).astype(np.int32), # col
1 # channel
]
pool_strides = [
1,
np.floor(shape[1] * 1. / l).astype(np.int32),
np.floor(shape[2] * 1. / l).astype(np.int32),
1
]
# 最大池化
pool = tf.nn.max_pool(input_, ksize=kernel_size, strides=pool_strides, padding='SAME')
# print("Pool Level {:}: shape {:}".format(l, pool.get_shape().as_list()))
h = int(pool.get_shape()[1])
w = int(pool.get_shape()[2])
d = int(pool.get_shape()[3])
# 池化结果的二维池化块拉成一维
pool = tf.reshape(pool,[-1])
pool = tf.reshape(pool,[-1, h * w, d, 1])
pool_outputs.append(pool)
# 将几个一维池化块拼接得到最终的SPP表示
spp_pool = tf.concat(pool_outputs, 1)
return spp_pool
池化不是必要操作
比如Stride Convolutional Layer可以代替池化层降采样,得到一个只含卷积操作的网络
论文:Striving for Simplicity: The All Convolutional Net(2015)
甚至也有论文表示CNN对微小平移和变形的稳定性与池化层无关,
参考论文 Learned Deformation Stability in Convolutional Neural Networks(2018)